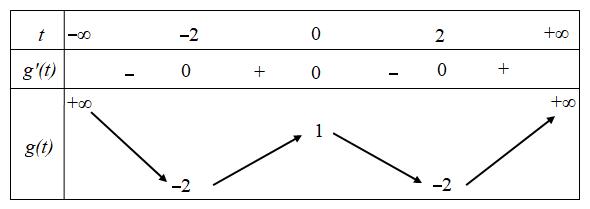
Cho hàm số f(x) có bảng biến thiên như sau: Gọi S là tập các giá trị t

Cho hàm số f(x) có bảng biến thiên như sau:

Gọi S là tập các giá trị thực của tham số m sao cho hàm số $\Large g(x)=\| 2 f(x)-2|+f(x)+10-m|$ có tổng giá trị nhỏ nhất và giá trị lớn nhất trên đoạn $\Large [-2;2]$ bằng 2. Tính tích các phần tử của S

• A. $\Large \dfrac{575}{4}$
• B. 154
• C. 156
• D. $\Large \dfrac{621}{4}$

Xét hàm số $\Large g(x)=\| 2 f(x)-2|+f(x)+10-m|$ trên đoạn $\Large [-2;2]$

Ta có: $\Large g(x)=\| 2 f(x)-2|+f(x)+10-m|=|-2 f(x)+2+f(x)+10-m|$ vì $\Large f(x) \leq 1 \forall x \in[-2 ; 2]$

Hay $\Large g(x)=|-f(x)+12-m|=|f(x)+m-12|$ trên đoạn $\Large [-2;2]$

Xét hàm số $\Large h(x)=f(x)+m-12$ trên đoạn $\Large [-2;2]$

Ta có bảng biến thiên

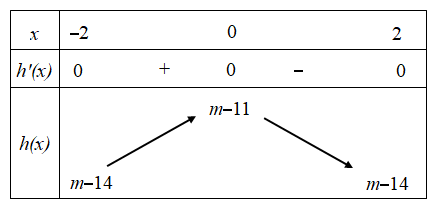
Suy ra $\Large \underset{(-2 ; 2]}{\operatorname{Max}} g(x)=\operatorname{Max}\{|m-14| ;|m-11|\}$

Theo yêu cầu bài toán ta có:

$\Large \underset{[-2 ; 2]}{\operatorname{Max}} g(x) \leq 2 \Leftrightarrow\left\{\begin{array}{l} |m-14| \leq 2 \\ |m-11| \leq 2 \end{array}\right.$ $\Large \Leftrightarrow\left\{\begin{array}{l} -2 \leq m-14 \leq 2 \\ -2 \leq m-11 \leq 2 \end{array} \Leftrightarrow\left\{\begin{array}{l} 12 \leq m \leq 16 \\ 9 \leq m \leq 13 \end{array} \Leftrightarrow 12 \leq m \leq 13\right.\right.$

Từ đó ta có: $\Large \left\{\begin{array}{l} m-11 > 0 \\ m-14 < 0 \end{array}\right.$. Nên $\Large \underset{[-2 ; 2]}{\operatorname{Min}} g(x)=0$ và $\Large \underset{[-2 ; 2]}{\operatorname{Max}} g(x)=2$

Suy ra: $\Large \left[\begin{array}{l} |m-14|=2 \\ |m-1|=2 \end{array}\right. \Leftrightarrow\left[\begin{array}{l} m=16 \\ m=12 \\ m=13 \\ m=9 \end{array}\right.$

Vì $\Large 12 \leq m \leq 13$ nên $\Large \left[\begin{array}{l} m=13 \\ m=12 \end{array}\right.$. Ta có: $\Large 12.13=156$