Cho hàm só f(x) liên tục trên $\Large \mathbb R$ và có đồ thị hàm số $

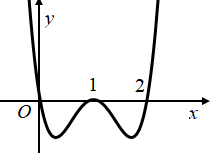
Cho hàm só f(x) liên tục trên $\Large \mathbb R$ và có đồ thị hàm số $\Large y=f'(x)$ như hình vẽ bên dưới

Hàm số $\Large g(x)=f\left(\dfrac{5 x}{x^{2}+4}\right)$ có bao nhiêu điểm cực đại?

• A. 1
• B. 2
• C. 0
• D. 3

Ta có: 

$\Large g^{\prime}(x)=\dfrac{5\left(x^{2}+4\right)-2 x \cdot 5 x}{\left(x^{2}+4\right)^{2}} f^{\prime}\left(\dfrac{5 x}{x^{2}+4}\right)=\dfrac{20-5 x^{2}}{\left(x^{2}+4\right)^{2}} f^{\prime}\left(\dfrac{5 x}{x^{2}+4}\right)$

$\Large g^{\prime}(x)=0 \Leftrightarrow \dfrac{20-5 x^{2}}{\left(x^{2}+4\right)^{2}} f^{\prime}\left(\dfrac{5 x}{x^{2}+4}\right)=0$

$\Large \Leftrightarrow\left[\begin{array}{l} \dfrac{20-5 x^{2}}{\left(x^{2}+4\right)}=0 \\ f^{\prime}\left(\dfrac{5 x}{x^{2}+4}\right)=0 \end{array}\right. \Rightarrow\left[\begin{array}{l} x^{2}=4 \\ \dfrac{5 x}{x^{2}+4}=0 \\ \dfrac{5 x}{x^{2}+4}=1 \\ \dfrac{5 x}{x^{2}+4}=2(V N) \end{array} \quad \Leftrightarrow\left[\begin{array}{l} x=\pm 2 \\ x=0 \\ x=1 \\ x=4 \end{array}\right.\right.$

Ta có BBT của hàm số $\Large y=g(x)$ :

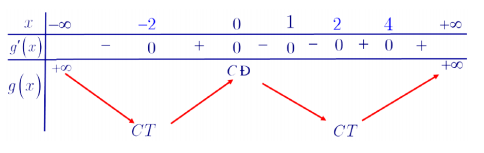
Từ BBT suy ra hoàm só $\Large g(x)=f\left(\dfrac{5 x}{x^{2}+4}\right)$ có 1 điểm cực đại