Cho hàm số $\Large y=f(x)$ liên tục trên $\Large \mathbb R$ và có đồ t

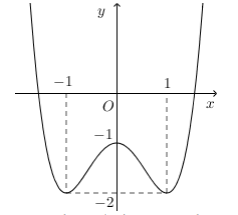
Cho hàm số $\Large y=f(x)$ liên tục trên $\Large \mathbb R$ và có đồ thị như hình vẽ

Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số $\Large y=f(\cos x)-2 \cos x-m$ cắt trục hoành tại điểm có hoành độ thuộc khoảng $\Large \left(-\dfrac{\pi}{2} ; \dfrac{\pi}{2}\right)$?

• A. 5
• B. 4
• C. 6
• D. 3

Phương trình hoành độ giao điểm của đồ thị hàm số $\Large y=f(\cos x)-2 \cos x-m$ và trục hoành là $\Large f(\cos x)-2 \cos x-m=0$ (1)

Đặt $\Large t=cos x$. Vì $\Large x \in\left(-\dfrac{\pi}{2} ; \dfrac{\pi}{2}\right)$ nên $\Large t \in(0,1]$. Phương trình (1) trở nào: $\Large f(t)-2 t=m(2)$ với $\Large t \in(0 ; 1]$. Bài toán đã cho trở thành: Tìm giá trị nguyên của m để phương tình (2) có nghiệm thuộc $\Large (0;1]$.

Xét hàm số $\Large g(t)=f(t)-2 t$, với $\Large t \in(0 ; 1]$, Ta có $\Large g^{\prime}(t)=f^{\prime}(t)-2$

Nhận xét: Dựa vào đồ thị hàm số $\Large y=f(x)$, ta có hàm số nghịch biến trong (0;1) và đạt cực trị tại $\Large x=1$ nên $\Large f^{\prime}(x) \leq 0, \forall x \in(0 ; 1]$, suy ra $\Large f^{\prime}(t) \leq 0, \forall t \in(0 ; 1]$.

Do đó $\Large g^{\prime}(t) < 0, \forall t \in(0 ; 1]$

Bảng biến thiên g(t)

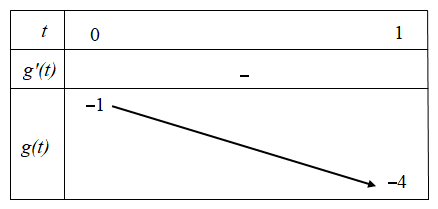
Dựa vào bảng biến thiên, suy ra phương trình (2) có nghiệm thuộc $\Large (0 ; 1] \Leftrightarrow-4 \leq m < -1$

Vì m nguyên nên $\Large m \in\{-4 ;-3 ;-2\}$. Vậy có 3 giá trị nguyên cua tham số m thỏa yêu cầu đề bài toán