Cho hàm số $\Large y=f(x)$ có đồ thị như hình vẽ: Gọi S là tập hợp các

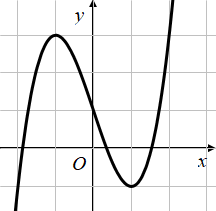
Cho hàm số $\Large y=f(x)$ có đồ thị như hình vẽ:

Gọi S là tập hợp các giá trị nguyên của tham số m để phương trình $\Large f(3 \sin x+m)-3=0$ có đúng 6 nghiệm phân biệt thuộc $\Large [0 ; 3 \pi]$. Tổng các phần tử của S bằng

• A. 0
• B. 1
• C. 2
• D. -1

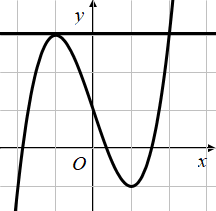
Ta có: $\Large f(3 \sin x+m)-3=0 \Leftrightarrow f(3 \sin x+m)=3$

Dựa vào đồ thị ta có: $\Large f(3 \sin x+m)=3 \Leftrightarrow\left[\begin{array}{l}
3 \sin x+m=-1 \\
3 \sin x+m=2
\end{array}\right.$ $\Large \Leftrightarrow\left[\begin{array}{l}
\sin x=\dfrac{-1-m}{3} \\
\sin x=\dfrac{2-m}{3}=1+\dfrac{-1-m}{3}
\end{array}\right.$

Ta có đồ thị hàm số $\Large y=\sin x$ trên $\Large [0;3\pi]$ như sau:

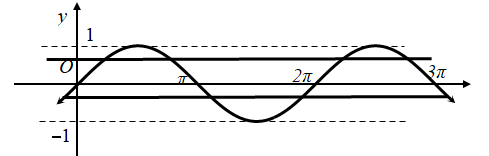
Dựa vào đồ thị ta có, để phương trình $\Large f(3 \sin x+m)-3=0$ có đúng 6 nghiệm phân biệt thuộc thì:

$\Large \left\{\begin{array}{l}
-1 < \dfrac{-1-m}{3} \leq 0 \\
0 < \dfrac{2-m}{3} \leq 1
\end{array} \Leftrightarrow-1 \leq m < 2\right.$

Mà $\Large m \in Z \Rightarrow\left[\begin{array}{l}
m=-1 \\
m=0 \Rightarrow S=0 \\
m=1
\end{array}\right.$