Cho hình chóp S.ABCD có đáy là hình chữ nhật, $\large AB= 2a,\, BC= a$

Cho hình chóp S.ABCD có đáy là hình chữ nhật, $\large AB= 2a,\, BC= a$. Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy là trung điểm của cnahj AB, góc giữa đường thẳng SC và mặt phẳng đáy bằng $\large 60^\circ $. Tính cosin góc giữa hai đường thẳng SB và AC

• A. A. $\large \dfrac{2}{\sqrt{7}}$
• B. B. $\large \dfrac{2}{\sqrt{35}}$
• C. C. $\large \dfrac{2}{\sqrt{5}}$
• D. D. $\large \dfrac{\sqrt{2}}{\sqrt{7}}$

Chọn B

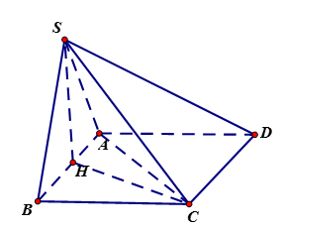
$\large \angle (SC, (ABCD))= \angle (SC, CH)= \widehat{SCH}= 60^\circ $
$\large \cos \widehat{SB, AC}= \dfrac{\left| \overrightarrow{SB}. \overrightarrow{AC}\right|}{SB. AC}$
$\large \overrightarrow{SB}. \overrightarrow{AC}= \left( \overrightarrow{SH}+ \overrightarrow{HB}\right)\left( \overrightarrow{AB}+\overrightarrow{BC}\right)$
$\large = \overrightarrow{SH}. \overrightarrow{AB}+ \overrightarrow{SH}. \overrightarrow{BC}+ \overrightarrow{HB}. \overrightarrow{AB}+ \overrightarrow{HB}. \overrightarrow{BC}$
$\large = \overrightarrow{HB}. \overrightarrow{AB}+ \overrightarrow{HB}. \overrightarrow{BC}= \dfrac{1}{2}AB^2= 2a^2$
$\large AC= a\sqrt{5},\, CH= \sqrt{a^2+a^2}= a\sqrt{2},\, SH= CH. \tan \widehat{SCH}= a\sqrt{6}$
$\large SB= \sqrt{SH^2+ HB^2}= \sqrt{\left( a\sqrt{6}\right)^2+ a^2}= a\sqrt{7}$
$\large \cos\widehat{SB, AC}= \dfrac{\left| \overrightarrow{SB}. \overrightarrow{AC}\right|}{SB. AC}= \dfrac{2a^2}{a\sqrt{7}. a\sqrt{5}}= \dfrac{2}{\sqrt{35}}$