Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh bằng a và góc A bằ

Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh bằng a và góc A bằng $\large 60^\circ $, cạnh SC vuông góc với đáy và $\large SC=\dfrac{a\sqrt{6}}{2}$. Giá trị lượng giác cosin của góc giữa hai mặt phẳng (SBD) và (SCD) bằng 

• A. A. $\large \dfrac{\sqrt{6}}{6}$
• B. B. $\large \dfrac{\sqrt{5}}{5}$
• C. C. $\large \dfrac{2\sqrt{5}}{5}$
• D. D. $\large \dfrac{\sqrt{30}}{6}$

Chọn A

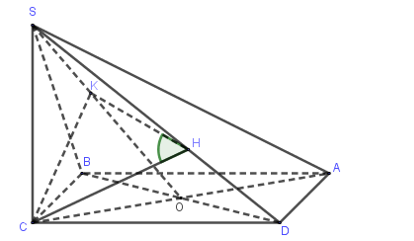
Từ $\large SC\perp (ABCD)\Rightarrow  SC\perp BD$
Từ $\large \left\{\begin{align}& BD\perp SC\\& BD\perp AC\\\end{align} \right.$ $\large \Rightarrow  BD\perp (SAC)$
Kẻ $\large CK\perp SO$, từ $\large BD\perp (SAC)\Rightarrow  BD\perp CK$. Như vậy $\large CK\perp (SBD)\Rightarrow  CK\perp SD$
Kẻ $\large CH\perp SD$, do $\large CK\perp SD$ nên suy ra $\large SD\perp (CHK)$
Mặt khác: $\large (CHK)\cap (SBD)= HK$ và $\large (CHK)\cap (SCD)= CK$ nên góc giữa hai mặt phẳng (SBD) và (SCD) bằng $\large \widehat{CHK}$
Trong tam giác SCD vuông tại C, ta có: 
$\large \dfrac{1}{CH^2}= \dfrac{1}{CD^2}+ \dfrac{1}{SC^2}= \dfrac{1}{a^2}+\dfrac{1}{\left( \dfrac{a\sqrt{6}}{2}\right)^2}= \dfrac{5}{3a^2}\Rightarrow  CH= \dfrac{a\sqrt{3}}{\sqrt{5}}$
Vì ABCD là hình thoi cạnh a và góc A bằng $\large 60^\circ $ nên $\large CO=\dfrac{a\sqrt{3}}{2}$
Trong tam giác SCO vuông tại C, ta có: 
$\large \dfrac{1}{CK^2}= \dfrac{1}{CO^2}+ \dfrac{1}{SC^2}= \dfrac{1}{\left( \dfrac{a\sqrt{3}}{2}\right)^2}+ \dfrac{1}{\left( \dfrac{a\sqrt{6}}{2}\right)^2}= \dfrac{2}{a^2}\Rightarrow  CK= \dfrac{a}{\sqrt{2}}$
Xét tam giác SHK vuông tại K, ta có: 
$\large HK=\sqrt{CH^2-CK^2}= \sqrt{\dfrac{3a^2}{5}-\dfrac{a}{2}}= \dfrac{a}{\sqrt{10}}$
$\large \co \widehat{CHK}= \dfrac{HK}{CH}= \dfrac{a}{\sqrt{10}}:\dfrac{a\sqrt{3}}{\sqrt{5}}= \dfrac{\sqrt{6}}{6}$
Vậy Cosin giữa hai mặt phẳng (SBD) và (SCD) bằng $\large \dfrac{\sqrt{6}}{6}$