Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, $\large $B

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, $\large $BC= a, cạnh bên SA vuông góc với đáy, $\large SA= a\sqrt{3}$. Gọi Ml à trung điểm của AC, tính cotan góc giữa hai mặt phẳng (SBM) và (SAB)

• A. A. $\large \dfrac{\sqrt{3}}{2}$
• B. B. $\large 1$
• C. C. $\large \dfrac{\sqrt{21}}{7}$
• D. D. $\large \dfrac{2\sqrt{7}}{7}$

Chọn A

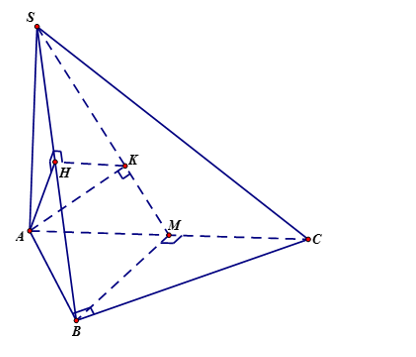
Kẻ $\large AH\perp SB$ và $\large AK\perp SM$
Vì tam giác ABC vuông cận tại B và $\large BC= a$ cùng với $\large SA\perp (ABC)$ nên suy ra $\large BM\perp (SAC)$ và $\large BM= AM=\dfrac{AC}{2}= \dfrac{a\sqrt{2}}{2}$. Do đó $\large BM\perp AK$
Từ $\large BM\perp AK$ và $\large AK\perp SM$ suy ra $\large AK\perp (SBM)\Rightarrow  AK\perp SB$
Từ $\large AH\perp SB$ và $\large AK\perp SB$ ta có: $\large (AHK)\perp SB$. Do đó góc giữa hai mặt phẳng (SBM) và (SAB) bằng hoặc bù với góc $\large \widehat{AHK}$
Ta có: 
$\large AH=\dfrac{SA.AB}{\sqrt{SA^2+ AB^2}}= \dfrac{a.a\sqrt{3}}{\sqrt{\left( a\sqrt{3}\right)^2+a^2}}= \dfrac{a\sqrt{3}}{2}$
$\large AK=\dfrac{SA.AM}{\sqrt{SA^2+ AM^2}}= \dfrac{\dfrac{a\sqrt{2}}{2}. a\sqrt{3}}{\sqrt{\left( a\sqrt{3}\right)^2+ \left( \dfrac{a\sqrt{2}}{2}\right)^2 }}= \dfrac{a\sqrt{21}}{7}$
Từ $\large (AHK)\perp SB$ ta có $\large HK\perp SB$ nên $\large \Delta SHK ~ \Delta SMB$, do đó $\large \dfrac{HK}{MB}= \dfrac{SK}{SB}$
Mặt khác:
$\large SK. SM= SA^2\Rightarrow  SK= \dfrac{SA^2}{SM}= \dfrac{\left( a\sqrt{3}\right)^2}{\left( a\sqrt{3}\right)^2+ \left( \dfrac{a\sqrt{2}}{2}\right)^2}= \dfrac{3a\sqrt{14}}{7};\, SB=\sqrt{SA^2+ AB^2}= 2a$
nên $\large \dfrac{HK}{MB} = \dfrac{SK}{SB}= \dfrac{3\sqrt{14}}{14}\Rightarrow  HK= \dfrac{3\sqrt{14}}{14}. MB= \dfrac{3\sqrt{14}}{14}. \dfrac{a\sqrt{2}}{2}= \dfrac{3a\sqrt{7}}{14}$
trong tam giác AHK có 
$\large \cos\widehat{AHK}= \dfrac{AH^2+HK^2-AK^2}{2.AH. HK}$
$\large \dfrac{\left( \dfrac{a\sqrt{3}}{2}\right)^2+ \left( \dfrac{3a\sqrt{7}}{14}\right)^2-\left( \dfrac{a\sqrt{21}}{7}\right)^2}{2. \dfrac{a\sqrt{3}}{2}. \dfrac{3a\sqrt{7}}{14}}= \dfrac{\sqrt{21}}{7}$
Như vậy góc giữa hai mặt phẳng (SBM) và (SAB) là $\large \alpha $ với $\large \cos\alpha = \dfrac{\sqrt{21}}{7}$
$\large \Rightarrow  \sin \alpha= \dfrac{a\sqrt{7}}{7}$. Bởi vậy $\large \cot\alpha= \dfrac{\cos\alpha}{\sin \alpha}= \dfrac{\sqrt{3}}{2}$