Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng 4a. Cạ

Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng 4a. Cạnh bên $\large SA= 2a$. Hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) là trung điểm H của đoạn thẳng AO. Gọi $\large \alpha $ là góc giữa SD và mặt phẳng (ABCD). Mệnh đề nào sau đây là đúng?

• A.

  $\large \tan\alpha = \sqrt{5}$

• B.

  $\large \tan\alpha = 1$

• C.

  $\large \tan\alpha = \dfrac{\sqrt{5}}{5}$

• D.

  $\large \tan\alpha = \sqrt{3}$

Chọn C

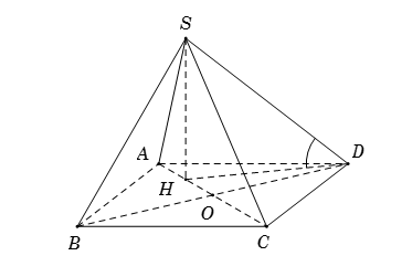
VÌ $\large SH\perp (ABCD)$ nên hình chiếu vuông góc của SD trên mặt phẳng (ABCD) là HD
Do đó: $\large (SD, (ABCD))= (SD, HD)= \widehat{SDH}$
Tính được $\large SH= \sqrt{SA^2-AH^2}= a\sqrt{2}$
Trong tam giác ADH có $\large DH= \sqrt{AH^2+AD^2-2.AH.AD.\cos 45^\circ }= a\sqrt{10}$
Tam giác vuông SHD, có $\large \tan \widehat{SDH}= \dfrac{SH}{HD}= \dfrac{\sqrt{5}}{5}$