Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, $\large AB=a,\

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, $\large AB=a,\, BC=a\sqrt{3}$. Hình chiếu vuông góc của S trên mặt đáy là trung điểm H của cạnh AC. Biết $\large SB= a\sqrt{2}$. Tính theo a khoảng cách từ điểm H đến mặt phẳng (SAB)?

• A. $\large \dfrac{7a\sqrt{21}}{3}$
• B. $\large \dfrac{a\sqrt{21}}{7}$
• C. $\large \dfrac{a\sqrt{21}}{3}$
• D. $\large \dfrac{3a\sqrt{21}}{7}$

Chọn B

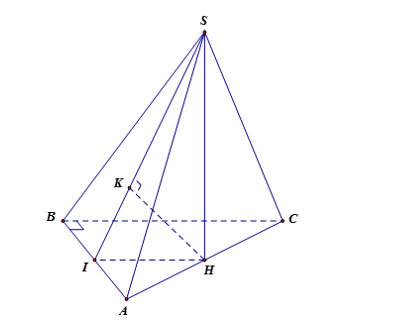
Để tính khoảng cách từ điểm H đến mặt phẳng (SAB), ta xác định hình chiếu vuông góc của H trên mặt phẳng (SAB) qua các bước sau:
-    Dựng $\large HI\perp AB$ với $\large I\in AB$, chứng minh được $\large AB\perp (SIH)$ và $\large (SIH)\perp (SAB)= SI$
-    Dựng K là hình chiếu vuông góc của H trên SI, ta chứng minh được $\large HK\perp (SAB)$
Vậy $\large d(H, (SAB))= HK$
Do $\large HI//BC$ nên dễ dàng chỉ ra được I là trung điểm của AB và $\large IH= \dfrac{BC}{2}= \dfrac{a\sqrt{3}}{2}$
$\large IA= IB= \dfrac{AB}{2}= \dfrac{a}{2}$
Ta có: $\large AB\perp SI$ nên $\large SI= \sqrt{SB^2-IB^2}= \sqrt{2a^2-\dfrac{a^2}{4}}= \dfrac{a\sqrt{7}}{2}$
Do $\large SH\perp IH$ nên xét tam giác vuông SIH có: 
$\large SH= \sqrt{SI^2-IH^2}= \sqrt{\dfrac{7a^2}{4}-\dfrac{3a^2}{4}}=a$
$\large HK= \dfrac{SH.HI}{SI} = \dfrac{a.\dfrac{a\sqrt{3}}{2}}{\dfrac{a\sqrt{7}}{2}}= \dfrac{a\sqrt{21}}{7}$

Do vậy, ta có: $\large d(H, (SAB))= \dfrac{a\sqrt{21}}{7}$