Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc vớ

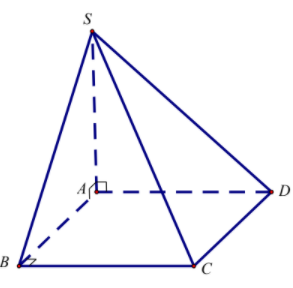
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và $\Large SA=a\sqrt{3}$ (tham khảo hình vẽ)

Góc giữa mặt phẳng (SBC) và (ABCD) bằng

• A. $\Large 30^{0}$
• B. $\Large 45^{0}$
• C. $\Large 60^{0}$
• D. $\Large 90^{0}$

Ta có $\Large (SBC)\cap (ABCD)=BC$. Do ABCD là hình vuông suy ra $\Large AB\perp BC(1)$ mà AB là hình chiếu vuông góc của SB lên (ABCD) nên $\Large SB\perp BC(2)$. Từ (1) và (2) suy ra góc giữa mặt phẳn (SBC) và (ABCD) bằng $\Large \widehat{SBA}$ (do tam giác $\Large \Delta SAB$ vuông tại A)

Ta có $\Large \tan\widehat{SBA}=\dfrac{SA}{AB}=\sqrt{3}$. Suy ra $\Large \widehat{SBA}=60^{0}$. Vậy góc giữa mặt phẳng (SBC) và (ABCD) bằng $\Large 60^{0}$