Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Tam giác SAB c

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Tam giác SAB cân tại S và (SAB) vuông góc với (ABCD). Giả sử thể tích của khối chóp S.ABCD là $\large \dfrac{4a^3}{3}$.Gọi $\large \alpha$ là góc tạo bởi SC và (ABCD). Tính $\large \cos\alpha$

• A.

  $\large \cos\alpha=\dfrac{\sqrt{3}}{2}$

• B.

  $\large \cos\alpha=\dfrac{\sqrt{30}}{6}$

• C.

  $\large \cos\alpha=\dfrac{\sqrt{14}}{4}$

• D.

  $\large \cos\alpha=\dfrac{\sqrt{5}}{3}$

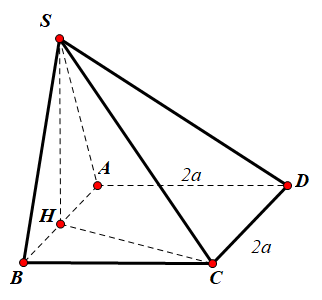
+) Gọi H là trung điểm của AB. Vì $\large \Delta SAB$ cân tại S nên $\large SH\perp AB$

+) Ta có: $\large \left\{\begin{align}& (SAB)\perp (ABCD)\\& (SAB)\cap (ABCD)=AB\\& SH\perp AH, SH\subset (SAB)\\\end{align}\right.$ $\large \Rightarrow SH \perp (ABCD)$

+) $\large V_{S.ABCD}=\dfrac{1}{3}SH. S_{ABCD}\Rightarrow SH=\dfrac{3V_{S.ABCD}}{S_{ABCD}}=\dfrac{3.\dfrac{4a^3}{3}}{4a^2}=a$

+) HC là hình chiếu của SC lên mp (ABCD) nên $\large \alpha =(\widehat{SC, HC})=\widehat{SCH}\Rightarrow \cos\alpha =\dfrac{HC}{SC}$

+) $\large HC=\sqrt{HB^2+BC^2}=a\sqrt{5}; SC=\sqrt{SH^2+HC^2}=a\sqrt{6}$. Suy ra: $\large \cos\alpha =\dfrac{a\sqrt{5}}{a\sqrt{6}}=\dfrac{\sqrt{30}}{6}$

Vậy $\large \cos\alpha=\dfrac{\sqrt{30}}{6}$