Cho hình chóp S.ABC có $\large SA = \dfrac{a\sqrt{3}}{2}$ , các cạnh c

Cho hình chóp S.ABC có $\large SA = \dfrac{a\sqrt{3}}{2}$, các cạnh còn lại cùng bằng a. Bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC là:

• A.

  A. $\large R = \dfrac{a\sqrt{13}}{2}$

• B.

  B. $\large R = \dfrac{a}{3}$

• C.

  C. $\large R = \dfrac{a\sqrt{13}}{3}$

• D.

  D. $\large R = \dfrac{a\sqrt{13}}{6}$

Chọn D. 

Cách 1:

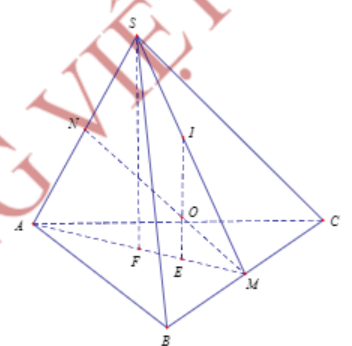
Gọi M, N lần lượt là trung điểm của BC và AD.

Ta có: $\large \Delta ABC$ và $\large \Delta SBC$ là các tam giác đều cạnh a $\large \Rightarrow AM = SM = \dfrac{a\sqrt{3}}{2}$. 

$\large \Delta SAM$ là tam giác đều cạnh $\large \dfrac{a\sqrt{3}}{2}$ 

Gọi F là trung điểm của AM $\large \Rightarrow SF \perp AM$   (1)

Mặt khác $\large \Delta ABC$ đều $\large \Rightarrow AM \perp BC$.

$\large \Delta SBC$ đều $\large \Rightarrow SM \perp BC$ 

$\large \Rightarrow BC \perp (SAM) \Rightarrow BC \perp SF$   (2)

Từ (1) và (2) $\large \Rightarrow SF \perp (ABC)$.

Gọi E là trọng tâm $\large \Delta ABC$ đều $\large \Rightarrow$ E là tâm đường tròn ngoại tiếp $\large \Delta ABC$.

Qua E kẻ đường thẳng (d) vuông góc với mp(ABC)

$\large \Rightarrow$ (d) là trục đường tròn ngoại tiếp $\large \Delta ABC$.

Vì $\large SF \perp (ABC) \Rightarrow (d) // SF$ 

Mặt khác $\large \Delta SAM$ đều nên đường thẳng MN là đường trung trực đoạn SA.

Trong mp (SAM), gọi $\large O = (d)\cap MN$ 

+ $\large O \in (d) \Rightarrow$ OA = OB = OC.

+ $\large O \in MN \Rightarrow$ OS = OA.

Vậy O là tâm mặt cầu ngoại tiếp hình chóp S.ABCD, bán kính $\large R = OA = \sqrt{OE^{2}+EA^{2}}$ 

Trong $\large \Delta ABC$: $\large AE = \dfrac{2}{3}AM = \dfrac{2}{3}.\dfrac{a\sqrt{3}}{2} = \dfrac{a\sqrt{3}}{3}$, 

$\large EM = \dfrac{1}{3}AM = \dfrac{a\sqrt{3}}{6}$.

$\large \Delta SAM$ đều $\large \Rightarrow$ MN là đường phân giác trong góc $\large \widehat{SMA} \Rightarrow \widehat{OME} = 30^{\circ}$.

Xét $\large \Delta OME$ vuông tại E: 

$\large tan30^{\circ} = \dfrac{OE}{EM} \Rightarrow OE = \dfrac{a\sqrt{3}}{6}.\dfrac{1}{\sqrt{3}} = \dfrac{a}{6}$.

Vậy $\large R = \sqrt{OE^{2}+EA^{2}} = \sqrt{\dfrac{a^{2}}{36}+\dfrac{a^{2}}{3}} = \dfrac{a\sqrt{13}}{6}$ 

Cách 2:

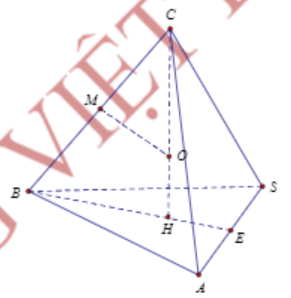
Gọi H là đường tròn ngoại tiếp tam giác SAB, E là trung điểm của SA.

$\large \Delta SAB$ cân tại B nên $\large H \in BE$.

Vì CA = CB = CS = a nên $\large CH \perp (SAB)$.

$\large \Rightarrow$ Đường thẳng CH là trục của đường tròn ngoại tiếp $\large \Delta SAB$

Gọi M là trung điểm của CB, qua M dựng đường thẳng (d) vuông góc với BC.

$\large (d)\cap CH = O$ .

$\large O \in (d) \Rightarrow OB = OC$.

$\large O \in CH \Rightarrow OS = OA = OB$.

Suy ra O là tâm mặt cầu ngoại tiếp hình chóp S.ABC, bán kính R = OC.

Ta có: 

$\large \Delta CMO \sim \Delta CHB \Rightarrow \dfrac{CM}{CH} =\dfrac{CO}{CB}$ 

$\large \Rightarrow CO = \dfrac{CM.CB}{CH} = \dfrac{CB^{2}}{2.CH}$

Xét $\large \Delta SBE$ ta có: 

$\large BE = \sqrt{SB^{2}-SE^{2}} = \sqrt{a^{2}-\dfrac{3a^{2}}{16}} = \dfrac{a\sqrt{13}}{4}$ 

Ta có: $\large S_{\Delta SAB} = \dfrac{1}{2}BE.SA = \dfrac{1}{2}.\dfrac{a\sqrt{13}}{4}.\dfrac{a\sqrt{3}}{2} = \dfrac{a^{2}\sqrt{39}}{16}$

Bán kính đường tròn ngoại tiếp $\large \Delta SAB$ là: 

$\large BH = \dfrac{SA.SB.AB}{4.S_{\Delta SAB}} = \dfrac{\dfrac{a^{3}\sqrt{3}}{2}}{4.\dfrac{a^{3}\sqrt{39}}{16}} = \dfrac{2a}{\sqrt{13}}$ 

Xét $\large \Delta CHB$ ta có: $\large \sqrt{CB^{2}-BH^{2}} = \sqrt{a^{2}-\dfrac{4a^{2}}{13}}= \dfrac{3a}{\sqrt{13}}$ 

Vậy $\large R = CO = \dfrac{CB^{2}}{2.CH} = \dfrac{a^{2}}{2.\dfrac{3a}{\sqrt{13}}} = \dfrac{a\sqrt{13}}{6}$