Cho hai mặt cầu $\large (S_{1})$ và $\large (S_{2})$ đồng tâm I , có b

Cho hai mặt cầu $\large (S_{1})$ và $\large (S_{2})$ đồng tâm I, có bán kính lần lượt là $\large R_{1}$ = 2 và $\large R_{2} = \sqrt{10}$. Xét tứ diện ABCD có hai đỉnh A, B nằm trên $\large (S_{1})$ và hai đỉnh C, D nằm trên $\large (S_{2})$. Thể tích lớn nhất của khối tứ diện ABCD bằng:

• A. A. $\large 3\sqrt{2}$
• B. B. $\large 7\sqrt{2}$
• C. C. $\large 4\sqrt{2}$
• D. D. $\large 6\sqrt{2}$

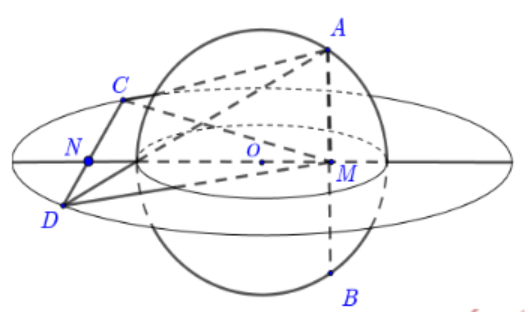
Ta có $\large V_{ABCD}= \dfrac{1}{6}AB.CD.d(AB,CD).sin(AB,CD)\Rightarrow V_{max}=\dfrac{1}{6}AB.CD.d(AB,CD)$ 

Khi đó AB $\large \perp$ CD. Gọi M, N lần lượt là trung điểm của AB và CD.

Đặt AM = x, CN = y. ($\large x \in (0;\sqrt{10}], y \in (0;2]$)

$\large \Rightarrow ON = \sqrt{10-x^{2}}$; $\large OM = \sqrt{4-y^{2}}$;

$\large d(AB,CD)= MN = OM+ON= \sqrt{10-x^{2}}+\sqrt{4-y^{2}}$ 

Khi đó $\large V_{ABCD}= \dfrac{1}{6}AB.CD.d(AB,CD)$

$\large = \dfrac{1}{6}2x.2y.\left ( \sqrt{10-x^{2}}+\sqrt{4-y^{2}} \right )$ 

$\large = \dfrac{2}{3}xy\left ( \sqrt{10-x^{2}}+\sqrt{4-y^{2}} \right )$.

Ta có: $\large V_{ABCD} = \dfrac{2}{3}xy.\left (\sqrt{2}\sqrt{\dfrac{10-x^{2}}{2}}+\sqrt{1}\sqrt{4-y^{2}}  \right )$

$\large \leq \dfrac{2}{3}xy\sqrt{(2+1)\left (\dfrac{10-x^{2}}{2}+4-y^{2}  \right )}$.

$\large V_{ABCD} \leq \dfrac{2}{3}xy\sqrt{\dfrac{3}{2}(18-(x^{2}+2y^{2}))}$

$\large \leq \dfrac{2}{3}xy\sqrt{\dfrac{3}{2}(18-2\sqrt{2}xy)}= \dfrac{2}{3}xy\sqrt{3(9-\sqrt{2}xy)}$ 

$\large \Rightarrow V_{ABCD}^{2} \leq \dfrac{4}{9}(xy)^{2}(3(9-\sqrt{2}xy))= \dfrac{8}{3}.\dfrac{xy}{\sqrt{2}}.\dfrac{xy}{\sqrt{2}}(9-\sqrt{2}xy)$

$\large \leq \dfrac{8}{3}\left (\dfrac{\dfrac{xy}{\sqrt{2}}+\dfrac{xy}{\sqrt{2}}+9-\sqrt{2}xy}{2}  \right )^{3}$ 

$\large \Rightarrow V_{ABCD}^{2} \leq \dfrac{8}{3}.\left (\dfrac{9}{3}  \right )^{3}=72\Rightarrow V_{ABCD}\leq 6\sqrt{2}$ .

Vậy $\large V_{max}= 6\sqrt{2}$. Dấu ''='' xảy ra khi:

$\large \begin{cases}
 & \ \dfrac{\sqrt{\dfrac{10-x^{2}}{2}}}{\sqrt{2}}=\dfrac{\sqrt{4-y^{2}}}{1} \\ 
 & \ \dfrac{xy}{\sqrt{2}}=9-\sqrt{2}xy 
\end{cases}\Rightarrow \begin{cases}
 & \ x= \sqrt{6}\\ 
 & \ y= \sqrt{3}
\end{cases}.$