Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, M là trung điể

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, M là trung điểm BC, hình chiếu vuông góc của S lên mặt phẳng (ABC) trùng với trung điểm của AM. Cho biết $\large AB=a; AC=a\sqrt{3}$ và mặt phẳng (SAB) tạo với mặt phẳng (ABC) một góc $\large 60^\circ$. Tính khoảng cách hai đường thẳng SA và BC .

• A.

  $\large \dfrac{a\sqrt{3}}{2}$

• B.

  $\large \dfrac{3a}{8}$

• C.

  $\large \dfrac{3a}{2}$

• D.

  $\large \dfrac{3a}{4}$

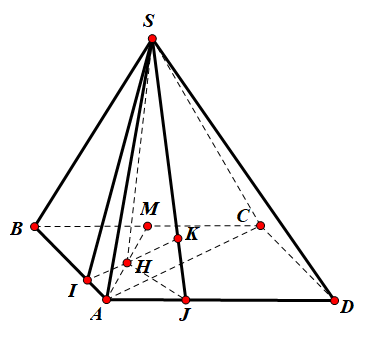
Dựng hình bình hành ABCD. Khi đó: 

$\large d(SA, BC)=d(BC, (SAD))=d(M, (SAD))=2d(H, (SAD))$ với H là trung điểm của AM

Theo bài ra ta suy ra: $\large SH\perp (ABCD)\Rightarrow SH\perp AD$

Kẻ $\large HJ\perp AD, HK\perp SJ\Rightarrow HK\perp (SAD)\Rightarrow d(H, (SAD))=HK$

Kẻ $\large HI\perp AB\Rightarrow SI\perp AB$, suy ra: $\large \widehat{((SAB), (ABC))}=\widehat{(SI, HI)}=\widehat{SIH}=60^\circ$

Dễ thấy $\large \Delta ABC\sim \Delta IAH$ suy ra: $\large \dfrac{AB}{IA}=\dfrac{BC}{AH}=\dfrac{BC}{\dfrac{BC}{4}}=4\Rightarrow AI=\dfrac{AB}{4}=\dfrac{a}{4}$

Tam giác $\large \Delta HIA$ vuông tại I $\large \Rightarrow IH=\sqrt{AH^2-IA^2}=\sqrt{\left(\dfrac{a}{2} \right )^2-\left(\dfrac{a}{4}\right)^2}=\dfrac{a\sqrt{3}}{4}$

Tam giác $\large \Delta SHI$ vuông tại H có $\large \widehat{SIH}=60^\circ\Rightarrow SH=IH.\tan 60^\circ=\dfrac{3a}{4}$

Ta có: $\large \Delta AJH\sim\Delta DCA\Rightarrow \dfrac{JH}{CA}=\dfrac{AH}{DA}=\dfrac{\dfrac{a}{2}}{2a}=\dfrac{1}{4}\Rightarrow JH=\dfrac{CA}{4}=\dfrac{a\sqrt{3}}{4}$

Tam giác $\large \Delta AHJ$ vuông tại H có đường cao HK: 

$\large \Rightarrow KH=\dfrac{SH.HJ}{\sqrt{SH^2+HJ^2}}=\dfrac{\dfrac{3a}{4}.\dfrac{a\sqrt{3}}{4}}{\sqrt{\left(\dfrac{3a}{4} \right )^2+\left(\dfrac{a\sqrt{3}}{4} \right )^2}}=\dfrac{3a}{8}\Rightarrow d(SA, BC)=2.\dfrac{3a}{8}=\dfrac{3a}{4}$