Cho hình chóp S ABCD . có đáy ABCD là hình vuông cạnh a, SA vuông góc

Cho hình chóp S ABCD . có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD), góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng $\large 45^\circ$. Khoảng cách giữa hai đường thẳng SB và AC bằng

• A. $\large \dfrac{4a}{7}$
• B. $\large \dfrac{2a}{5}$
• C. $\large \dfrac{a\sqrt{10}}{5}$
• D. $\large \dfrac{a\sqrt{10}}{7}$

Chọn C

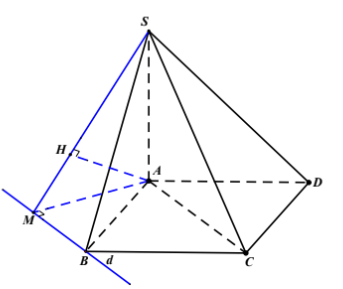
Ta có: $\large SA\perp (ABCD) \Rightarrow AC$ là hình chiếu vuông góc của SC lên (ABCD)

$\large \Rightarrow $ Góc giữa SC và (ABCD) bằng $\large \widehat{SCA} = 45^\circ\Rightarrow SA= AC= \sqrt{2} a$

Kẻ đường thằng d qua B và song song với AC

Gọi M là hình chiếu vuông góc của A trên d, H là hình chiếu vuông góc của A trên SM

Ta có: $\large SA\perp BM,\, MS\perp BM$ nên $\large AH\perp BM\Rightarrow AH\perp (SBM)$

Do đó: $\large d(AC, SB) = d(A, (SBM)) = AH$

Tam giác SAM vuông tại A, có đường cao AH, nên $\large \dfrac{1}{AH^2} = \dfrac{1}{SA^2} + \dfrac{1}{AM^2} = \dfrac{5}{2a^2}$

Vậy $\large d(AC, SB) = AH = \dfrac{a\sqrt{10}}{5}$