Cho hàm số $\large f(x) =\dfrac{ax+b}{cx+1},\, (a,b,c\in \mathbb{R}) $

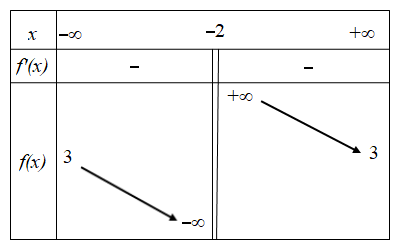
Cho hàm số $\large f(x) =\dfrac{ax+b}{cx+1},\, (a,b,c\in \mathbb{R})  $ có bảng biến thiên như sau: 

Trong các số a, b và c có bao nhiêu số dương?

• A. 3
• B. 0
• C. 1
• D. 2

Chọn A

Ta có: $\large f'(x)   = \dfrac{a-bc}{(cx+1)^2},\forall x\neq -\dfrac{1}{c}$

Từ BBT ta thấy, đồ thị có tiệm cận đứng $\large x= -2$ và tiệm cận ngang $\large y = 3$ và hàm số nghịch biến trên từng khoảng xác định nên $\large \left\{\begin{align}& -\dfrac{1}{c} < 0 \,\, (1)\\& \dfrac{a}{c} > 0 \,\, (2) \\& a-bc < 0 \,\, (3) \\\end{align}\right. $

Từ (1), (2) và (3) suy ra $\large c> 0, a> 0, b> 0$