Cắt hình nón đỉnh S bởi một mặt phẳng đi qua trục ta được thiết diện l

Cắt hình nón đỉnh S bởi một mặt phẳng đi qua trục ta được thiết diện là tam giác SAB vuông cân có cạnh huyền bằng $\large a\sqrt{2}$. Gọi C là một điểm thuộc đường tròn đáy hình nón sao cho mặt phẳng (SBC) tạo với mặt phẳng chứa đáy hình nón một góc $\large 60^\circ$. Diện tích của tam giác SBC bằng

• A. $\large \dfrac{a^2\sqrt{3}}{4}$
• B. $\large \dfrac{a^2\sqrt{5}}{3}$
• C. $\large \dfrac{a^2\sqrt{5}}{2}$
• D. $\large \dfrac{a^2\sqrt{2}}{3}$

Chọn D

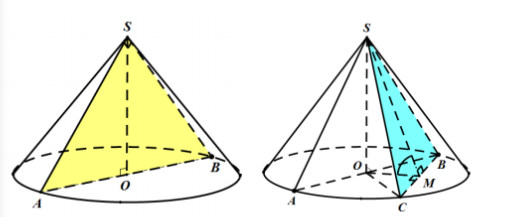
Gọi O là tâm của đường tròn đáy. Giả sử mặt phẳng đi qua trục SO của hình nón và cắt hình nón theo một thiết diện là tam giác $\large \Delta SAB$ vuông cân tại S có cạnh huyền $\large AB = a\sqrt{2}$

Ta có: $\large \Delta SAB$ vuông cân tại S nên $\large SO = OA= OB = \dfrac{AB}{2} = \dfrac{a\sqrt{2}}{2} ,\, r = OB = \dfrac{AB}{2} = \dfrac{a\sqrt{2}}{2}$

Gọi M là trung điểm của BC

Ta có: $\large \left\{\begin{align}& (SBC)\cap (OBC) = BC\\& OB\subset (OBC),\, OM\perp BC\\& AM\subset (SBC),\, SM\perp BC\\\end{align}\right.$

$\large \Rightarrow$ Góc giữa hai mặt phẳng (SBC) và (OBC) bằng $\large (SM, OM) = \widehat{SMO } = 60^\circ$

Vì $\large \Delta SMO$ vuông tại O nên $\large SM = \dfrac{SO}{\sin \widehat{SMO}}= \dfrac{a\sqrt{2}}{2}:\sin 60^\circ = \dfrac{a\sqrt{6}}{3}$ và $\large OM = SM.\cos\widehat{SMO} = \dfrac{a\sqrt{6}}{3}.\cos 60^\circ = \dfrac{a\sqrt{6}}{3}.\dfrac{1}{2} = \dfrac{a\sqrt{6}}{6}$

Ta có lại có: $\large \Delta OBM$ vuông tại M nên $\large BM = \sqrt{OB^2 - OM^2} = \sqrt{\left(\dfrac{a\sqrt{2}}{2}\right)^2 - \left(\dfrac{a\sqrt{6}}{6}\right)^2}= \dfrac{a\sqrt{3}}{3}$

Suy ra: $\large BC= 2BM = \dfrac{2a\sqrt{3}}{3}$

Vậy diện tích $\large \Delta SBC$ là $\large S = \dfrac{1}{2}.\dfrac{a\sqrt{6}}{3}.\dfrac{2a\sqrt{3}}{3} = \dfrac{a^2\sqrt{2}}{3}$