Cho hình chóp S. ABC có $\large SA\perp (ABCD),\, SA= 2a$. Tam giác AB

Cho hình chóp S. ABC có $\large SA\perp (ABCD),\, SA= 2a$. Tam giác ABC vuông tại B có $\large AB= a,\, BC=a\sqrt{3}$. Tính cosin của góc $\large $ tạo bởi hai mặt phẳng (SAC) và (SBC)

• A. A. $\large \cos\varphi = \sqrt{\dfrac{3}{5}}$
• B. B. $\large \cos\varphi = \sqrt{\dfrac{1}{5}}$
• C. C. $\large \cos\varphi = \sqrt{\dfrac{2}{3}}$
• D. D. $\large \cos\varphi = \sqrt{\dfrac{1}{3}}$

Chọn A

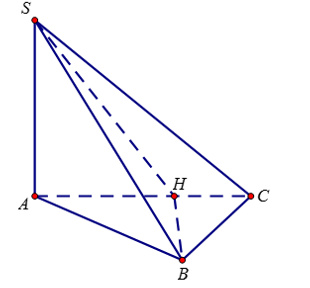
Kẻ $\large BH\perp AC\Rightarrow  BH\perp (SAC)$. Áp dụng công thức $\large S’=S.\cos \phi $ trong đó $\large S’= dt(SHC)$
$\large S= st(SBC),\, \phi $ là góc hợp bởi hai mặt phẳng (SBC) và (SAC)
Dễ thấy tam giác SBC vuông tại B, và $\large SB= a\sqrt{5}.dt(SBC)=\dfrac{a^2\sqrt{15}}{2}$
$\large CH= \dsf{BC^2}{AC}= \dfrac{3}{2}a,\, dt(SHC)=\dfrac{3}{2}a^2$
Vậy $\large \cos\phi= \dfrac{\sqrt{15}}{5}$
Cách khác: 
Gắn hình chóp vào hệ trục tọa độ như hình vẽ sao cho
$\large A(a, 0, 0),\, B(0, 0, 0),\, S(a, 0, 2a), C(0, a\sqrt{3}, 0)$
$\large \overrightarrow{SA}= (0, 0, -2a)\to $ chọn $\large \overrightarrow{u_1}= (0; 0; 1)$ cùng phương với $\large \overrightarrow{SA}$
$\large \overrightarrow{SC}= (-a; a\sqrt{3}; -2a)\to $ chọn $\large \overrightarrow{u_2}$ cùng phương với $\large \overrightarrow{SC}$
$\large \overrightarrow{SB}= (-a; 0; -2a)\to $ chọn $\large \overrightarrow{u_3}$ cùng phương với $\large \overrightarrow{SB}$
$\large \overrightarrow{n_{SAC}}= \left[\overrightarrow{u_1}; \overrightarrow{u_2} \right]= \left(-\sqrt{3}; -1; 0 \right)$
$\large \overrightarrow{n_{SBC}}= \left[ \overrightarrow{u_2}; \overrightarrow{u_3}\right]= \left( 2\sqrt{3}; 0; -\sqrt{3}\right)$
$\large \cos\varphi = \dfrac{\left| \overrightarrow{n_{(SAC)}}. \overrightarrow{n_{(SBC)}}\right|}{\left| \overrightarrow{n_{(SAC)}\right|. \left| \overrightarrow{n_{(SBC)}\right|}= \dfrac{6}{2\sqrt{15}}= \sqrt{\dfrac{3}{5}}$