Cho hình hộp chữ nhật $\large ABCD.A_1B_1C_1D_1$ có ba kích thước $\la

Cho hình hộp chữ nhật $\large ABCD.A_1B_1C_1D_1$ có ba kích thước $\large AB=a,\, AD=2a,\, AA_1= 3a$. Khoảng cách từ A đến mặt phẳng ($\large A_1BD_1 $) bằng bao nhiêu 

• A. A. $\large a$
• B. B. $\large \dfrac{7}{6}a$
• C. C. $\large \dfrac{a\sqrt{2}}{2}$
• D. D. $\large \dfrac{6}{7}a$

Chọn D

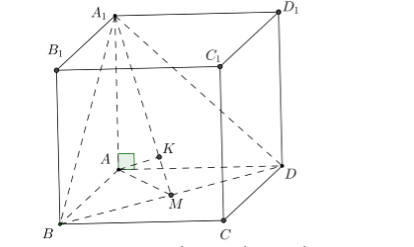
Trong tam giác ABD kẻ $\large AM\perp BD$ suy ra $\large \dfrac{1}{AM^2}= \dfrac{1}{AB^2}+ \dfrac{1}{AD^2}$
Trong tam giác $\large A_1AM$ kẻ $\large AK\perp A_1M$
$\large \Rightarrow  \dfrac{1}{AK^2}= \dfrac{1}{AA_1^2}+\dfrac{1}{AM^2}= \dfrac{1}{a^2}+ \dfrac{1}{4a^2}+\dfrac{1}{9a^2}\Rightarrow  AK=\dfrac{6}{7}a$
Khi đó: $\large AK\perp (A_1BD)$ hay $\large d(A, (A_1BD))= AK=\dfrac{6}{7}a$