Cho hình chóp S. ABCD có đáy ABCD là hình thoi tâm O, đương thẳng SO v

Cho hình chóp S. ABCD có đáy ABCD là hình thoi tâm O, đương thẳng SO vuông góc với mặt phẳng (ABCD). Biết $\large BC= SB= a,\, SO= \dfrac{a\sqrt{6}}{3}$. Tìm số đo góc giữa hai mặt phẳng (SBC) và (SCD)

• A. A. $\large 90^\circ $
• B. B. $\large 60^\circ $
• C. C. $\large 45^\circ $
• D. D. $\large 30^\circ $

Chọn A

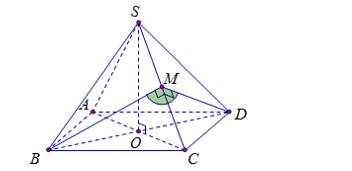
Gọi M là trung điểm của SC, do tam giác SBC cân tại B nên ta có $\large SC\perp BM$ (1)
Theo giả thiết ta có: $\large BD\perp (SAC)\Rightarrow  SC\perp BD$. Do đó $\large SC\perp BCM)$ suy ra $\large SC\perp DM$ (2)
Từ (1) và (2) suy ra góc giữa hai mặt phẳng (SBC) và (SCD) là góc giữa hai đường thẳng BM và DM
Ta có: $\large \Delta SBO= \Delta CBO$ suy ra $\large SO= CO= \dfrac{a\sqrt{6}}{3}$
Do đó: $\large OM= \dfrac{1}{2}SC= \dfrac{a\sqrt{3}}{3}$
Mặt khác: $\large OB= \sqrt{SB^2- SO^2}= \dfrac{a\sqrt{3}}{3}$. Do đó tam giác BMO vuông cân tại M hay $\large \widehat{BMO}= 45^\circ $, suy ra $\large \widehat{BMD}= 90^\circ $
Vậy $\large \angle ((SBC), (SCD))= 90^\circ  $