Cho hình chóp S.ABCDS.ABCD có đáy ABCDABCD là hình vuông cạnh

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCDS.ABCD có đáy ABCDABCD là hình vuông cạnh a,a, SA=2aSA=2a và vuông góc với (ABCD).(ABCD). Gọi MM là trung điểm của SD.SD. Tính khoảng cách dd giữa hai đường thẳng SBSB và CM.CM.
Đáp án án đúng là: C
Lời giải chi tiết:
Chọn C
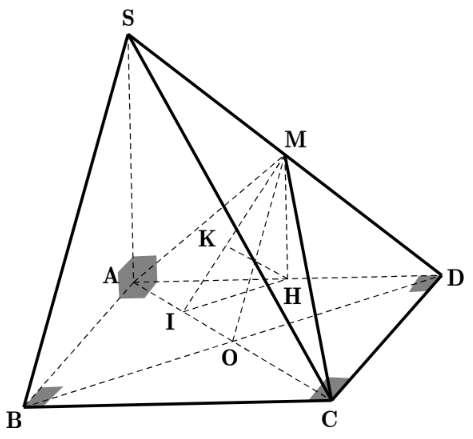
Gọi O=AC∩BD.O=AC∩BD.
Vì ABCDABCD là hình vuông cạnh aa
⇒O⇒O là trung điểm của BDBD
Mà MM là trung điểm của SDSD
⇒OM//SB⇒OM//SB ⇒SB//(ACM).⇒SB//(ACM).
Do đó d(SB,CM)=d(SB,(ACM))d(SB,CM)=d(SB,(ACM)) =d(B,(ACM))=d(B,(ACM)) =d(D,(ACM)).=d(D,(ACM)).
Gọi HH là trung điểm của ADAD ⇒MH//SA⇒MH//SA ⇒MH⊥(ABCD).⇒MH⊥(ABCD).
Khi đó ta có: d(SB,CM)=d(D,(ACM))=2d(H,(ACM)).d(SB,CM)=d(D,(ACM))=2d(H,(ACM)).
Kẻ HI⊥AC⇒(MHI)⊥(MAC)HI⊥AC⇒(MHI)⊥(MAC) theo giao tuyến MI.MI.
Kẻ HK⊥MI⇒HK⊥(ACM)HK⊥MI⇒HK⊥(ACM) ⇒d(H,(ACM))=HK.⇒d(H,(ACM))=HK.
HI=12OD=14BD=14√AB2+AD2=a√24HI=12OD=14BD=14√AB2+AD2=a√24
MH=12SA=a.MH=12SA=a.
1HK2=1HM2+1HI21HK2=1HM2+1HI2 ⇔1HK2=1a2+1(a√24)2⇔1HK2=1a2+1(a√24)2 ⇔1HK2=9a2⇔1HK2=9a2 ⇔HK=a3.⇔HK=a3.
Vậy d(SB,CM)=2d(H,(ACM))=2HK=2a3.d(SB,CM)=2d(H,(ACM))=2HK=2a3.
Xem thêm các bài tiếp theo bên dưới
- Cho hàm số y=f(x)y=f(x) thỏa mãn $\Large \big[{f}'(x)\big]^2+f(x).{
- Một hình trụ có bán kính đáy bằng chiều cao và bằng a.a. Một hì
- Giả sử (x0;y0)(x0;y0) là một nghiệm của phương trình $\Large 4^{x
- Cho hình hộp ABCD.A′B′C′D′ có các cạnh bằng 2a. Biết
- Cho hàm số y=|x4−2x3+x2+a|. Có bao nhiêu số thực $\Large a