Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình thang vuông

Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình thang vuông tại $\Large A$ và $\Large B$. Biết $\Large AD=2a$, $\Large AB=BC=a$ và $\Large SA$ vuông góc với mặt đáy $\Large (ABCD)$, $\Large SA=a\sqrt{2}$. Gọi $\Large M$ trung điểm của $\Large AD$. Khoảng cách giữa hai đường thẳng $\Large BM$ và $\Large SC$ bằng

• A.

  $\Large a\sqrt{2}$.

• B.

  $\Large a$.

• C.

  $\Large 2a$.

• D.

  $\Large \dfrac{a}{2}$.

Chọn D

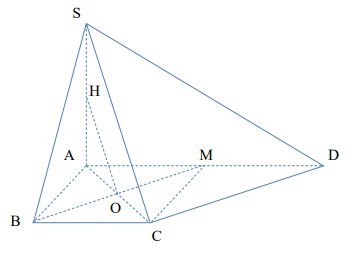
Gọi $\Large O$ là tâm của hình vuông $\Large ABCM$, $\Large H$ là trung điểm của $\Large SA\Rightarrow HO$ song song với $\Large SC$ 

Nên $\Large SC$ song song với mặt phẳng $\Large (HBM)$$\Large \Rightarrow d_{[SC; BM]}$=$\Large d_{[SC, (HBM)]}$=$\Large d_{[C, (HBM)]}$=$\Large d_{[A, (HBM)]}$

Xét tứ diện vuông $\Large AHBM$ ta có: $\Large \dfrac{1}{d^2_{[C, (HBM)]}}=\dfrac{1}{AH^2}+\dfrac{1}{AB^2}+\dfrac{1}{AM^2}$ $\Large \Rightarrow d_{[C, (HBM)]}=\dfrac{a}{2}$.