Cho phương trình $\Large \mathrm{log}_6(2018x+m)=\mathrm{log}_4(1009x)

Cho phương trình $\Large \mathrm{log}_6(2018x+m)=\mathrm{log}_4(1009x)$. Số giá trị nguyên của tham số $\Large m$ nhỏ hơn 2020 để phương trình có nghiệm là

• A. 2022.
• B. 2021.
• C. 2019.
• D. 2020.

Chọn A
Điều kiện: $\Large \left\{\begin{align} & 2018x+m > 0 \\ & x > 0 \end{align}\right.$

Đặt $\Large \mathrm{log}_6(2018x+m)=\mathrm{log}_4(1009x)=t$ $\Large \Leftrightarrow \left\{\begin{align} & 2018x+m=6^t (1)\ \\ & 1009x=4^t\ (2) \end{align}\right.$

Thế (2) vào (1) ta được ta được $\Large 2.4^t=m=6^t$ $\Large \Leftrightarrow m=6^t-2.4^t$

Xét hàm số $\Large f(t)=6^t-2.4^t$

Ta có: $\Large {f}'(t)=6^t\mathrm{ln}6-2.4^t\mathrm{ln}4$

Có $\Large {f}'(t)=0$ $\Large \Leftrightarrow 6^t\mathrm{6}-2.4^t\mathrm{ln}4=0$ $\Large \Leftrightarrow \left(\dfrac{2}{3}\right)^t=\dfrac{\mathrm{ln}6}{2\mathrm{4}}$ $\Large \Leftrightarrow t=\mathrm{log}_{\frac{2}{3}}\left(\dfrac{\mathrm{ln}6}{2\mathrm{4}}\right)$

Bảng biến thiên

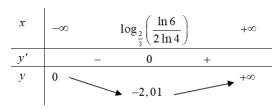
Để phương trình có nghiệm thì $\Large m\geq -2,01$

Vì $\Large m$ là các số nguyên nhỏ hơn 2020 nên $\Large m\in \begin{Bmatrix} -2; -1; 0; 1;...; 2019 \end{Bmatrix}$ 

Vậy có 2022 số nguyên $\Large m$ thỏa mãn.