Xét các số thực $\Large a$, $\Large b$ thỏa mãn $\Large a > 1$, $\Larg

Xét các số thực $\Large a$, $\Large b$ thỏa mãn $\Large a > 1$, $\Large b > 1$. Biết phương trình $\Large a^xb^{x^2}=b^2$ có hai nghiệm phân biệt $\Large x_1$, $\Large x_2$. Giá trị nhỏ nhất của biểu thức $\Large S=\left(\dfrac{x_1x_2}{x_1+x_2}\right)^2-4(x_1+x_2)$ thuộc tập nào dưới đây?

• A.

  $\Large (3; 4)$.

• B.

  $\Large (6; 7]$.

• C.

  $\Large \left[\dfrac{15}{2}; 8\right)$.

• D.

  $\Large [8; 9)$.

Chọn C

Theo bài ra:

$\Large \mathrm{log}_a(a^xb^{x^2})=\mathrm{log}_bb^2$

$\Large \Leftrightarrow x.\mathrm{log}_ba+x^2=2$

$\Large \Leftrightarrow x^2+x.\mathrm{log}_ba-2=0$

Đặt $\Large \mathrm{log}_ba=t (t > 0)$ ta được phương trình mới:

$\Large x^2+x.t-2=0$

Vì $\Large \Delta=t^2+8 > 0 \forall t > 0$ nên phương trình trên luôn có 2 nghiệm phân biệt.

Theo định lí Vi-et: $\Large \left\{\begin{align} & x_1+x_2=-t \\ & x_1x_2=-2 \end{align}\right.$

Thay vào biểu thức S ta có:

$\Large S=\left(\dfrac{-2}{-t}\right)^2-4.(-t)=\dfrac{4}{t^2}+4t=4\left(\dfrac{1}{t^2}+t\right)$

$\Large {S}'=4\left(1-\dfrac{2}{t^3}\right)$

$\Large {S}'=0 \Leftrightarrow \dfrac{2}{t^3}=1\Leftrightarrow t^3=2\Leftrightarrow t=\sqrt[3]{2}$

(Thỏa mãn điều kiện $\Large t > 0$)

Lập bảng biến thiên:

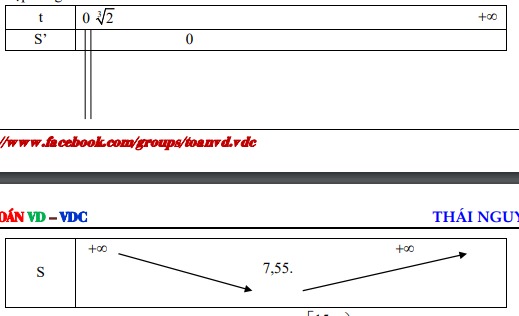
Quan sát bảng biến thiên, ta được $\Large S_{min}=7,55..\in \left[\dfrac{15}{2}; 8\right)$