Cho hàm số $\Large y=f(x)$ có đồ thị như hình vẽ bên. Số nghiệm của ph

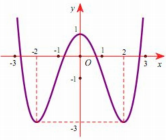
Cho hàm số $\Large y=f(x)$ có đồ thị như hình vẽ bên. Số nghiệm của phương trình $\Large 2f(2cos2x)+1=0$ trong $\Large \left[-\dfrac{\pi}{4}; \pi\right]$ là

• A. 3.
• B. 4.
• C. 5.
• D. 6.

Chọn C

Ta có $\Large 2f(2cos2x)+1=0$ $\Large \Leftrightarrow f(2cos2x)=-\dfrac{1}{2}$

Đặt $\Large t=2cos2x$, vì $\Large -1\leq cos2x\leq 1$ $\Large \Leftrightarrow -2\leq 2cos2x \leq 2$ $\Large \Leftrightarrow -2 \leq t \leq 2$ 

Khi đó phương trình trở thành $\Large f(t)=-\dfrac{1}{2}$

Nghiệm của phương trình $\Large f(t)=-\dfrac{1}{2}$ là hoành độ giao điểm của đồ thị hàm số $\Large y=f(t)$ và đường thẳng $\Large y=-\dfrac{1}{2}$

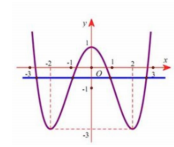
Dựa vào đồ thị hàm số ta có $\Large f(t)=-\dfrac{1}{2}$ $\Large \Leftrightarrow \left[\begin{align} & t=a_1 (-3 < a_1 < -2) \\ & t=a_2 (-1 < a_2 < 0) \\ & t=a_3 (0 < a_3 < 1) \\ & t=a_4 (2 < a_4 < 3) \end{align}\right.$

Ta thấy $\Large t=a_1$, $\Large t=a_4$ không thỏa mãn 

Với $\Large t=a_2$, $\Large t=a_3$

Xét hàm số $\Large t=cos2x$

Ta có $\Large {t}'=-2sin2x$

Có $\Large {t}'=0$ $\Large \Leftrightarrow sin2x=0\Leftrightarrow x=\dfrac{k\pi}{2}$. Vì $\Large x\in \left[-\dfrac{\pi}{4}; \pi\right]$ nên $\Large x=0$, $\Large x=\dfrac{\pi}{2}$

BẢNG BIẾN THIÊN

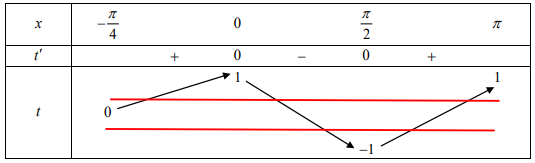
Dựa vào BBT ta thấy phương trình $\Large cos2x=a_2$ có 2 nghiệm, phương trình $\Large cos2x=a_3$ có 3 nghiệm.
Vậy phương trình đã cho có 5 nghiệm.