Cho khối $\Large ABCD.{A}'{B}'{C}'{D}'$, $\Large M$ là trung điểm của

Cho khối $\Large ABCD.{A}'{B}'{C}'{D}'$, $\Large M$ là trung điểm của $\Large {C}'{D}'.N$ là điểm trên cạnh $\Large AD$ sao cho $\Large DN=2AN$. Mặt phẳng $\Large ({B}'MN)$ chia khối hộp thành hai phần có thể tích lần lượt là $\Large V_1$; $\Large V_2$ thỏa mãn $\Large V_1 < V_2$. Tỉ lệ $\Large \dfrac{V_1}{V_2}$ bằng

• A.

  $\Large \dfrac{1}{3}$.

• B.

  $\Large \dfrac{47}{135}$.

• C.

  $\Large \dfrac{47}{88}$.

• D.

  $\Large \dfrac{88}{135}$.

Chọn C

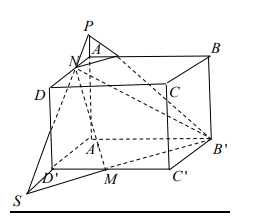
Gọi $\Large V_1$ là thể tích hình chứa cạnh $\Large A{A}'$

Dễ dàng chứng minh được $\Large \dfrac{P{A}'}{A{A}'}=\dfrac{6}{5}$; $\Large V_{A.{A}'{B}'{C}'{D}'}=\dfrac{1}{3}V_{hop}$; $\Large V_1=\dfrac{6}{5}V_{A{A}'{B}'{C}'{D}'}$.

Suy ra: $\Large V_1=\dfrac{1}{3}.\dfrac{6}{5}.\left(1-\dfrac{1}{6^3}-\dfrac{1}{2^3}\right)=\dfrac{47}{135}$ $\Large \dfrac{V_1}{V_2}=\dfrac{47}{88}$.