Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình thang vuông

Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình thang vuông tại $\Large A$ và $\Large D$, $\Large AB=AD=2a$, $\Large DC=a$. Điểm $\Large I$ là trung điểm đoạn $\Large AD$, mặt phẳng $\Large (SIB)$ và $\Large (SIC)$ cùng vuông góc với mặt phẳng $\Large (ABCD)$. Mặt phẳng $\Large (SBC)$ tạo với mặt phẳng $\Large (ABCD)$ một góc $\Large 60^{\circ}$. Tính khoảng cách từ $\Large D$ đến $\Large (SBC)$ theo $\Large a$.

• A.

  $\Large \dfrac{a\sqrt{15}}{5}$.

• B.

  $\Large \dfrac{9a\sqrt{15}}{10}$.

• C.

  $\Large \dfrac{2a\sqrt{15}}{5}$.

• D.

  $\Large \dfrac{9a\sqrt{15}}{20}$.

Chọn A

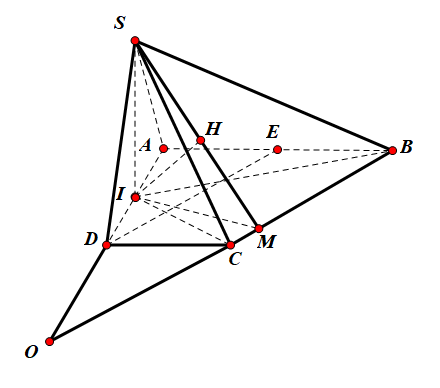
Từ giả thuyết ta có $\Large SI\perp (ABCD)$.

Kẻ $\Large IM\perp BC$ tại điểm $\Large M$.

$\Large \Rightarrow SM\perp BC$

$\Large \Rightarrow \left(\widehat{(SBM);(ABCD)}\right)=\widehat{SMI}=60^{\circ}$.

Gọi $\Large O=AD\cap BC$, ta có $\Large \dfrac{d\left(D; (SBC)\right)}{d\left(I; (SBC)\right)}=\dfrac{OD}{OI}=\dfrac{2}{3}$$\Large \Rightarrow d\left(D; (SBC)\right)=\dfrac{2}{3}d\left(I; (SBC)\right)$.

$\Large BC\perp (SIM)\Rightarrow (SIM)\perp (SBC)$ theo giao tuyến $\Large SM$.

Trong $\Large (SIM)$, kẻ $\Large IH\perp SM\Rightarrow IH\perp (SBC)$.

Tứ giác $\Large BCDE$ là hình bình hành $\Large \Rightarrow BC=DE=\sqrt{AD^2+AE^2}=a\sqrt{5}$

$\Large S_{IBC}=S_{ABCD}-S_{AIB}-S_{DIC}=\dfrac{3a^2}{2}$.

Mà $\Large S_{IBC}=\dfrac{1}{2}BC.IM$$\Large \Rightarrow IM=\dfrac{2.S_{IBC}}{BC}=\dfrac{3a\sqrt{5}}{5}$.

Xét tam giác vuông $\Large HIM$ ta có $\Large IH=IM.sin60^{\circ}=\dfrac{3a\sqrt{15}}{10}$

Vậy $\Large d\left(D; (SBC)\right)=\dfrac{2}{3}IH=\dfrac{a\sqrt{15}}{5}$.