Cho mặt cầu $\Large (S)$ tâm $\Large O$ và các điểm $\Large A$, $\Larg

Cho mặt cầu $\Large (S)$ tâm $\Large O$ và các điểm $\Large A$, $\Large B$, $\Large C$ nằm trên mặt cầu $\Large (S)$ sao cho $\Large AB=3$, $\Large AC=4$, $\Large BC=5$ và khoảng cách từ $\Large O$ đến mặt phẳng $\Large (ABC)$ bằng 1. Thể tích của khối cầu $\Large (S)$ bằng 

• A.

  $\Large \dfrac{20\sqrt{5}\pi}{3}$.

• B.

  $\Large \dfrac{7\sqrt{21}\pi}{2}$.

• C.

  $\Large \dfrac{29\sqrt{29}\pi}{6}$.

• D.

  $\Large \dfrac{4\sqrt{17}\pi}{3}$.

Chọn C

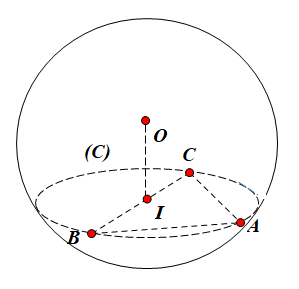
Giả sử mặt phẳng $\Large (ABC)$ cắt mặt cầu $\Large (S)$ theo giao tuyến là đường tròn $\Large (C)$. Tam giác $\Large ABC$ có $\Large AB^2+AC^2=BC^2$ nên là tam giác vuông tại $\Large A$, suy ra tâm $\Large I$ của $\Large (C)$ là trung điểm của $\Large BC$ và là hình chiếu của $\Large O$ trên $\Large (ABC)$. Theo giả thiết ta có $\Large OI=1$. Vậy bán kính của mặt cầu $\Large (S)$ là: $\Large R=OC=\sqrt{OI^2+IC^2}=\sqrt{1+\dfrac{25}{4}}=\dfrac{\sqrt{29}}{4}$.

Thể tích của khối cầu $\Large (S)$ là: $\Large V=\dfrac{4}{3}\pi R^3=\dfrac{4}{3}\pi \left(\dfrac{\sqrt{29}}{2}\right)^3$=$\Large \dfrac{29\pi \sqrt{29}}{6}$.