Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. M

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M là trung điểm SA biết AD=a√3,AB=a. Khi đó khoảng cách từ C đến (MBD) là
Đáp án án đúng là: B
Lời giải chi tiết:
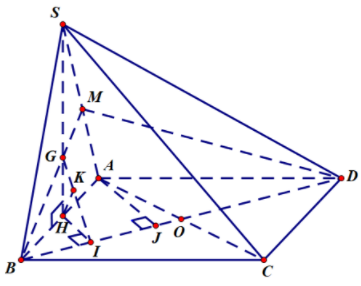
Gọi H là trung điểm của AB⇒SH⊥AB⇒SH⊥(ABCD) (Vì (SAB)⊥(ABCD))
Gọi G là trọng tâm tam giác SAB, suy ra G là là giao điểm của SH và BM
Gọi O là giao điểm của AC và BD , suy ra O là trung điểm của AC
⇒d(C;(MBD))=d(A;(MBD))
Từ H kẻ HI⊥BD, ta có {BD⊥HIBD⊥SH⇒BD⊥(SHI)⇒(MBD)⊥(SHI)
Từ H kẻ HK⊥GI⇒HK⊥(MBD)⇒HK=d(H;(MBD))
Gọi AJ là đường cao trong ΔABD⇒1AJ2=1AB2+1AD2=1a2+13a2=43a2⇒AJ=a√32
Ta có: HI=12AJ=a√34;HG=13HS=a√36
Xét ΔGHI ta có: 1HK2=1HI2+1HG2=163a2+363a2=523a2⇒HK=a√3926
Do H là trung điểm của AB ⇒d(A;(MBD))=2d(H;(MBD))=2HK=a√3913
Vậy d(C;(MBD))=d(A;(MBD))=a√3913
Xem thêm các bài tiếp theo bên dưới