Cho hai hàm số $\large y = x^{6} + 6x^{4} + 6x^{2} + 1$ và $\large y =

Cho hai hàm số $\large y = x^{6} + 6x^{4} + 6x^{2} + 1$ và $\large y = x^{3} \sqrt {m -15x} (m + 3 - 15x)$ có đồ thị lần lượt là $\large (C1)$ và $\large (C2)$. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc đoạn [-2020; 2020] để $\large (C1)$ và $\large (C2)$ cắt nhau tại hai điểm phân biệt. Số phần tử của tập hợp $\large S$ bằng

• A.

  2010

• B.

  2009

• C.

  2008

• D.

  2007

Ta biết $\large (C1)$ và $\large (C2)$ tại hai điểm phân biệt khi và chỉ khi phương trình
$\large  x^{6} + 6x^{4} + 6x^{2} + 1 =  x^{3} \sqrt {m -15x} (m + 3 - 15x)$    (1) có hai nghiệm phân biệt.
Điều kiện: $\large m - 15x \geq 0 \Leftrightarrow m \geq 15x$   (*)
Nếu $\large x = 0$ thì phương trình (1) vô nghiệm. Suy ra $\large x \neq 0$
Khi đó (1) $\large \Leftrightarrow x^{3} + 6x + \dfrac{6}{x} + \dfrac {1}{x^{3}} =\sqrt {m -15x} (m + 3 - 15x)$
$\large \Leftrightarrow (x + \dfrac {1}{x})^{3} + 3 (x + \dfrac {1}{x}) = (\sqrt {m - 15x})^{3} + 3 \sqrt{m - 15x}$
Xét hàm số $\large f(t) = t^{3} + 3t$. Tập xác định $\large D = \mathbb{R}$
$\large f'(t) = 3t^{2} + 3 > 0$, với mọi $\large t \in \mathbb{R}$. Suy ra hàm số $\large f (t) = t^{3} + 3t$ đồng biến trên $\large \mathbb{R}$.
Do đó (1) $\large \Leftrightarrow x + \dfrac {1}{x} = \sqrt {m - 15x}$  (2)
Nếu $\large x < 0 \Rightarrow  x + \dfrac {1}{x} < 0 \Rightarrow$ Phương trình (2) vô nghiệm $\large \Rightarrow x > 0$
Khi đó $\large \left\{\begin{matrix} m > 0 \\ x + \dfrac {1}{x} > 0 \end{matrix}\right.$ nên (2) $\large \Leftrightarrow x^{2} + \dfrac {1}{x^{2}} + 2 = m - 15x \Leftrightarrow m = x^{2} + \dfrac {1}{x^{2}} + 2 + 15x$
Đặt $\large g(x) = x^{2} + \dfrac {1}{x^{2}} + 2 + 15x, x > 0.$ $\large g'(x)=2x - \dfrac {2}{x^{3}} + 15$
Phương trình $\large g'(x) = 0$ có một nghiệm $\large x = \dfrac{1}{2}$ trên khoảng $\large (0; +\infty)$
Bảng biến thiên

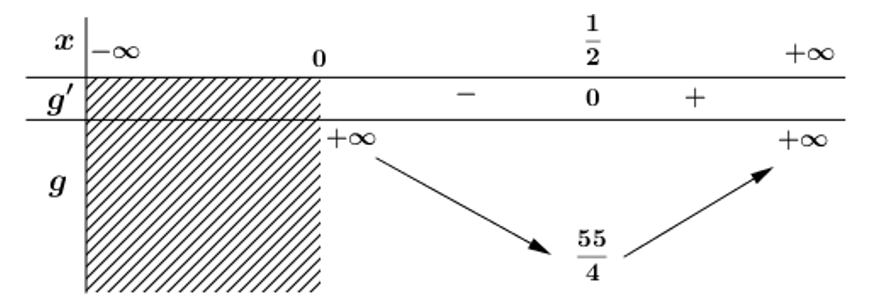
Suy ra (1) có hai nghiệm phân biệt khi và chỉ khi $\large m > \dfrac {55}{4}$ (thỏa mãn $\large m > 0$).

Kết hợp với m nguyên và $\large m \in [-2020; 2020]$ ta có được $\large m$ nguyên và $\large m \in [14; 2020]$. Khi đó $\large S = 2020 -14 + 1 = 2007$ phần tử.