Cho hình chóp S.ABCD có đáy là hình chữ nhật, mặt bên $\large
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCD có đáy là hình chữ nhật, mặt bên SAD là tam giác vuông tại S. Hình chiếu vuông góc của S trên mặt đáy là điểm H thuộc cạnh AD sao cho HA=3HD. Biết rằng SA=2a√3 và SC tạo với mặt phẳng đáy một góc bằng 30∘. Thể tích của khối chóp đã cho bằng:
Đáp án án đúng là: C
Lời giải chi tiết:
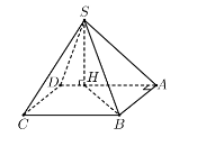
Xác định: 30∘=(^SC,(ABCD))=(^SC,HC)=^SCH
Tam giác vuông SAD, có SA2=AH⋅AD⇔12a2=34AD⋅AD
Suy ra AD=4a,HA=3a,HD=a,SH=√HA.HD=a√3
HC=SH.cot^SCH=3a,CD=√HC2−HD2=2a√2
Diện tích hình chữ nhật: SABCD=AD.CD=8√2a
Vậy thể tích khối chóp: VS.ABCD=13SABCD⋅SH=8√6a33.
Chọn C.
Xem thêm các bài tiếp theo bên dưới