Cho hình chóp $\Large S.ABC$ có $\Large SA$ vuông góc với mặt phẳng $\

Cho hình chóp $\Large S.ABC$ có $\Large SA$ vuông góc với mặt phẳng $\Large (ABC)$, $\Large SA=1$ và đáy $\Large ABC$ là tam giác đều với độ dài cạnh bằng 2. Tính góc giữa mặt phẳng $\Large (SBC)$ và mặt phẳng $\Large (ABC)$.

• A.

  $\Large 60^{\circ}$.

• B.

  $\Large 45^{\circ}$.

• C.

  $\Large 30^{\circ}$.

• D.

  $\Large 90^{\circ}$.

Chọn C

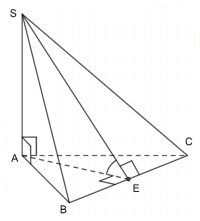
+ Gọi $\Large E$ là trung điểm của $\Large BC$. Ta có tam giác $\Large ABC$ đều nên $\Large AE\perp BC$ (1).

$\Large SA\perp (ABC)\Rightarrow SA\perp BC$ (2)

Từ (1) và (2) ta suy ra $\Large BC\perp (SAE)$ $\Large \Rightarrow BC\perp SE$.

+ Ta có $\Large \left\{\begin{align} & (SBC)\cap (ABC)=BC \\ & SE\subset (SBC), SE\perp BC \\ & AE\subset (ABC), AE\perp BC \end{align}\right.$

$\Large \Rightarrow$ Góc giữa mặt phẳng $\Large (SBC)$ và mặt phẳng $\Large (ABC)$ là $\Large \widehat{(AE, SE)}=\widehat{SEA}$ (do $\Large SA\perp (ABC)\Rightarrow SA\perp AE$ $\Large \Rightarrow \widehat{SEA}$ nhọn).

+ Tam giác $\Large ABC$ đều với độ dài cạnh bằng 2, $\Large AE\perp BC$ $\Large \Rightarrow AE=\dfrac{BC\sqrt{3}}{2}=\sqrt{3}$.

+ Tam giác $\Large SAE$ vuông tại $\Large A$ nên $\Large tan\widehat{SEA}=\dfrac{SA}{AE}=\dfrac{1}{\sqrt{3}}$ $\Large \Rightarrow \widehat{SEA}=30^{\circ}$.

Vây góc giữa mặt phẳng $\Large (SBC)$ và mặt phẳng $\Large (ABC)$ bằng $\Large 30^{\circ}$.