Cho hình chóp $\Large S.ABC$ có $\Large SA$ vuông góc với mặt phẳng đá

Cho hình chóp $\Large S.ABC$ có $\Large SA$ vuông góc với mặt phẳng đáy. Biết góc $\Large \widehat{BAC}=30^{\circ}, SA=a$ và $\Large BA=BC=a.$ Gọi $\Large D$ là điểm đối xứng của $\Large B$ qua $\Large AC.$ Khoảng cách từ $\Large B$ đến mặt phẳng $\Large (SCD)$ bằng

• A.

  A. $\Large \dfrac{\sqrt{17}}{51}a.$

• B.

  B. $\Large \dfrac{\sqrt{21}}{7}a.$

• C.

  C. $\Large \dfrac{\sqrt{17}}{68}a.$

• D.

  D. $\Large \dfrac{\sqrt{51}}{51}a.$

Chọn B

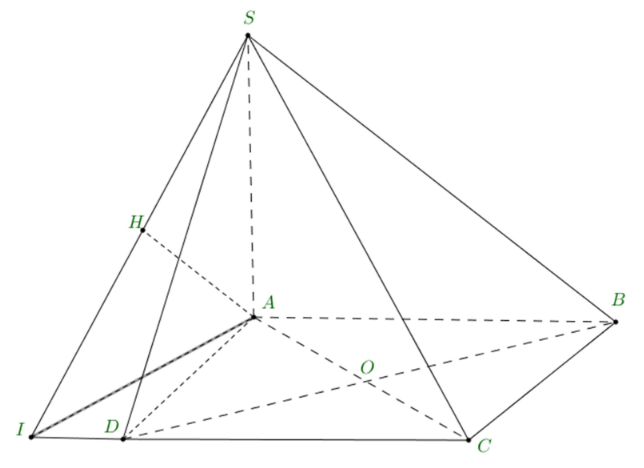
Ta có $\Large ABCD$ là hình thoi.

$\Large d(B; (SCD))=d(A; (SCD))$
Kẻ $\Large AI\perp DC, AH\perp SI,$ ta có $\Large AH\perp (SCD).$

Suy ra $\Large d(A; (SCD))=AH.$

$\Large S_{\Delta ACD}=\dfrac{1}{2}DA.DC.\sin{120}^{\circ}=\dfrac{1}{2}AI.DC.$
Suy ra $\Large AI=DA.\sin{120}^{\circ}=\dfrac{a\sqrt{3}}{2}.$
$\Large \dfrac{1}{AH^2}=\dfrac{1}{AI^2}+\dfrac{1}{AS^2}=\dfrac{4}{3a^2}+\dfrac{1}{a^2} \Rightarrow AH=\dfrac{a\sqrt{3}}{\sqrt{7}}.$
Vậy $\Large d(B; (SCD))=\dfrac{a\sqrt{21}}{7}.$