Cho hàm số $\Large y=f(x)$ liên tục trên $\Large \mathbb{R}$ và có bản

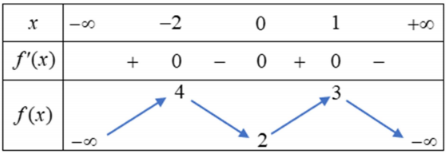
Cho hàm số $\Large y=f(x)$ liên tục trên $\Large \mathbb{R}$ và có bảng biến thiên như hình bên.

Số điểm cực trị của hàm số $\Large y=|3f(x)-7|$ là

• A.

  A. $\Large 7.$

• B.

  B. $\Large 11.$

• C.

  C. $\Large 5.$

• D.

  D. $\Large 9.$

Chọn A

Xét hàm số $\Large g(x)=3f(x)-7.$

$\Large {g}'(x)=3{f}'(x).$

Suy ra bảng biến thiên như sau:

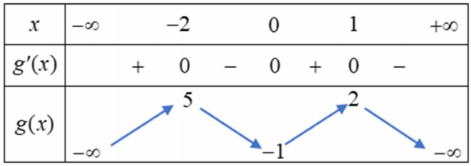
Suy ra hàm số $\Large g(x)=3f(x)-7$ có ba điểm cực trị và đồ thị hàm số cắt trục $\Large Ox$ tại bốn điểm phân biệt có hoành độ $\Large \notin \begin{Bmatrix}
-2, 0, 1
\end{Bmatrix}.$ Do đó số điểm cực trị của hàm số $\Large y=|3f(x)-7|$ bằng $\Large 7.$