Khối lăng trụ $\Large ABC.A'B'C'$ có thể tích $\Large V=12.$ Gọi $\Lar

Khối lăng trụ $\Large ABC.A'B'C'$ có thể tích $\Large V=12.$ Gọi $\Large D, E, M$ lần lượt là trung điểm các cạnh $\Large A'C', CC'$ và $\Large BC.$ Mặt phẳng $\Large (DEM)$ chia khối lăng trụ thành 2 khối đa diện. Tính thể tích của khối đa diện không chứa điểm $\Large A.$

• A.

  A. $\Large 5.$

• B.

  B. $\Large 6.$

• C.

  C. $\Large 10.$

• D.

  D. $\Large 8.$

Chọn B

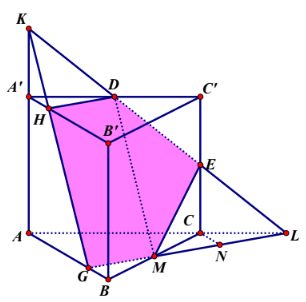
+) Trong mặt phẳng $\Large (ACC'A')$ kéo dài $\Large DE$ cắt $\Large AC$ và $\Large AA'$ tại $\Large L$ và $\Large K.$ Trong mặt phẳng $\Large (ABC)$, kéo dài $\Large LM$ cắt $\Large AB$ tại $\Large G.$ Nối $\Large G$ với $\Large K$ cắt $\Large A'B'$ tại $\Large H.$ Khi đó $\Large (DEM)$ chia lăng trụ thành 2 phần. 

+) Gọi $\Large V_1, V_2$ lần lượt là thể tích khối đa diện chứa đỉnh $\Large A$, khối đa diện chứa đỉnh $\Large B$ (không chứa đỉnh $\Large A$) như hình vẽ.

+) Ta có $\Large K{A}'={C}'E=CE \Rightarrow \dfrac{{K}'A}{KA}=\dfrac{KD}{KL}=\dfrac{1}{3}.$

+) $\Large \dfrac{V_{K.AGL}}{V_{{A}'.AGL}}=\dfrac{3}{2} \Rightarrow V_{K.AGL}=\dfrac{3}{2}V_{{A}'.AGL}.$

+) Kẻ $\Large CN//AB, N\in GL \Rightarrow BG=CN$

$\Large \Rightarrow \dfrac{BG}{AG}=\dfrac{CN}{AG}=\dfrac{LC}{LA}=\dfrac{LE}{LK}=\dfrac{1}{3}$ $\Large \Rightarrow \dfrac{BG}{AB}=\dfrac{1}{4}$

$\Large \Rightarrow S_{\Delta AGL}=\dfrac{AG}{AB}.\dfrac{AL}{AC}.S_{\Delta ABC}$ $\Large =\dfrac{3}{4}.\dfrac{3}{2}.S_{\Delta ABC}$ $\Large =\dfrac{9}{8}S_{\Delta ABC}$

$\Large \dfrac{V_{A'.AGL}}{V_{A'.ABC}}=\dfrac{9}{8} \Rightarrow V_{{A}'.AGL}=\dfrac{9}{24}V$ $\Large \Rightarrow V_{K.AGL}=\dfrac{3}{2}.\dfrac{9}{24}V=\dfrac{9}{16}V.$
$\Large +) \dfrac{V_{K.{A}'HD}}{V_{K.AGL}}=\dfrac{1}{27}; \dfrac{V_{L.ECM}}{V_{L.KAG}}=\dfrac{1}{3}.\dfrac{1}{3}.\dfrac{2}{3}=\dfrac{2}{27}$
$\Large \Rightarrow V_1=V_{K.AGL}-V_{K.{A}'HD}-V_{L.ECM}$ $\Large =\dfrac{8}{9}V_{K.AGL}$ $\Large =\dfrac{8}{9}.\dfrac{9}{16}V$ $\Large =\dfrac{1}{2}V$

$\Large  \Rightarrow V_2=\dfrac{1}{2}V.$
Vậy thể tích phần khối đa diện không chứa điểm $\Large A$ là $\Large V_2=\dfrac{1}{2}.12=6.$