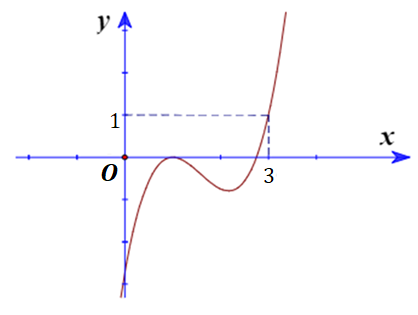
Cho hàm số $\Large f(x)=ax^3+bx^2+cx+d$ có đồ thị như hình vẽ bên. Gọi

Cho hàm số $\Large f(x)=ax^3+bx^2+cx+d$ có đồ thị như hình vẽ bên.

Gọi $\Large S$ là tập hợp tất cả các giá trị của $\Large m$ để bất phương trình $\Large (x-3)\big[m^3f(2x-3)-mf(x)+f(x)-1\big] \geq 0$ nghiệm đúng $\Large \forall x \in \mathbb{R}.$ Số phần tử của tập $\Large S$ là

• A.

  A. $\Large 4.$

• B.

  B. $\Large 2.$

• C.

  C. $\Large 3.$

• D.

  D. $\Large 1.$

Bất phương trình $\Large (x-3)\big[m^3f(2x-3)-mf(x)+f(x)-1\big] \geq 0 \ (1)$ nghiệm đúng $\Large \forall x \in \mathbb{R}$ thì $\Large x=3$ là nghiệm của phương trình $\Large m^3f(2x-3)-mf(x)+f(x)-1=0$

$\Large \Rightarrow m^3f(3)-mf(3)+f(3)-1=0$ $\Large \Leftrightarrow \left[\begin{align} & m=0 \\ & m=\pm 1 \end{align}\right.$

Dựa vào đồ thị suy ra:

+) $\Large x \leq 3 \Rightarrow 2x-3 \leq 3$ $\Large \Rightarrow \left\{\begin{align} & f(x) \leq 1 \\ & f(2x-3) \leq 1 \end{align}\right.$

+) $\Large x \geq 3 \Rightarrow 2x-3 \geq 3$ $\Large \Rightarrow \left\{\begin{align} & f(x) \geq 1 \\ & f(2x-3) \geq 1 \end{align}\right.$

- Với $\Large m=0$ $\Large \Rightarrow  (1) \Leftrightarrow (x-3)\big[f(x)-1\big] \geq 0, \forall x \in \mathbb{R}.$

- Với $\Large m=1$ $\Large \Rightarrow (1) \Leftrightarrow (x-3) \left[ f(2x-3)-1 \right] \geq 0, \forall x \in \mathbb{R}.$

- Với $\Large m=-1$ $\Large \Rightarrow (1) \Leftrightarrow (x-3)\big[-f(2x-3)+2f(x)-1\big] \geq 0$

$\Large \underset{x\rightarrow -\infty}{\lim}(x-3)\big[-a(2x-3)^3-b(2x-3)^2-c(2x-3)-d+2ax^3+2bx^2+2cx+2d-1\big]$ $\Large =\underset{x\rightarrow -\infty}{\lim}(x-3)\big[-6ax^3+(36a-2b)x^2+(12b-54a)x+d+27a-9b+3c-1\big]$ $\Large =-\infty (a > 0)$ (loại)

Vậy có $\Large 2$ giá trị của $\Large m$ thỏa mãn yêu cầu bài toán.