Cho hình chóp $\Large S.ABC$ có đáy $\Large ABC$ là tam giác đều, cạnh

Cho hình chóp $\Large S.ABC$ có đáy $\Large ABC$ là tam giác đều, cạnh bên $\Large SA$ vuông góc với mặt phẳng đáy và $\Large SA=\sqrt{3}$, góc giữa $\Large (SBC)$ với đáy $\Large (ABC)$ bằng $\Large 45^{\circ}$. Thể tích khối chóp $\Large S.ABC$ bằng

• A.

  $\Large \dfrac{\sqrt{3}}{4}$.

• B.

  $\Large \sqrt{3}$.

• C.

  $\Large 1$.

• D.

  $\Large \dfrac{\sqrt{3}}{12}$.

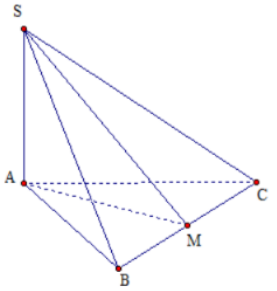
Gọi $\Large M$ là trung điểm của $\Large BC$, từ giả thiết suy ra: $\Large \left\{\begin{align} & BC\perp AM\\ & BC\perp SA \end{align}\right.$ $\Large \Rightarrow BC\perp (SAM)\Rightarrow BC\perp SM$.

Suy ra: $\Large \left\{\begin{align} & (SBC)\cap (ABC)=BC\\ & BC\perp AM, AM\subset (ABC)\Rightarrow SMA=(MS; MA)=\left((ABC); (SBC)\right)=45^{\circ}\\ & BC\perp SM, SM\subset (SBC)\end{align}\right.$

Tam giác $\Large SAM$ vuông cân tại $\Large A$, suy ra: $\Large AM=SA=\sqrt{3}$.

Mặt khác: $\Large AM=\dfrac{BC\sqrt{3}}{2}\Leftrightarrow \sqrt{3}=\dfrac{BC\sqrt{3}}{2}\Leftrightarrow BC=2$.

Vậy $\Large V_{S.ABC}=\dfrac{1}{6}SA.AM.BC=\dfrac{1}{6}\sqrt{3}.\sqrt{3}.2=1$.