Giá trị của $\Large m$ để hàm số $\Large y = \dfrac{1}{3}x^{3} - mx^{2

Giá trị của $\Large m$ để hàm số $\Large y = \dfrac{1}{3}x^{3} - mx^{2} + (m^{2} - 4)x + 5$

 đạt cực tiểu tại điểm $\Large x = 1$ là:

• A.

  A. $\Large m = 1$

• B.

  B. $\Large m = -1$

• C.

  C. $\Large m = -3$

• D.

  D. $\Large m = 0$

Chọn B

Ta có:

$\Large y{}' = x^{2} - 2mx + m^{2} - 4$

Phương trình $\Large y{}' = 0$ 

$\Large \Leftrightarrow x^{2} - 2mx + m^{2} - 4 = 0$ 

$\Large \Leftrightarrow \left[\begin{array}{l}x= m - 2 \\x = m + 2 \\\end{array}\right.$

Bảng biến thiên của hàm số như sau:

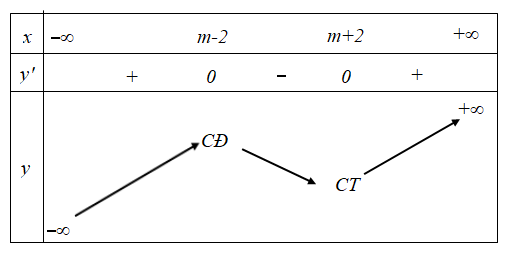
Từ bảng biến thiên ta có hàm số đạt cực tiểu tại $\Large x = 1 \Leftrightarrow m + 2 = 1 \Leftrightarrow m = -1$.