Cho lăng trụ tam giác đều ABC.A′B′C′<script type="math/tex" id="MathJax-Element-1">\Large ABC.{A}'{B}'{C}'</script> có diện tích đáy b

Cho lăng trụ tam giác đều $\Large ABC.{A}'{B}'{C}'$ có diện tích đáy b

Bài sau

4.5/5

Tác giả: Thầy Tùng

Đăng ngày: 18 Aug 2022

Lưu về Facebook:

$Hình minh họa Cho lăng trụ tam giác đều $\Large ABC.{A}'{B}'{C}'$ có diện tích đáy b$

MỤC LỤC

Câu hỏi

Lời giải chi tiết

Câu hỏi:

Cho lăng trụ tam giác đều $\Large ABC.{A}'{B}'{C}'$ có diện tích đáy bằng $\Large \sqrt{3}a^2$ , diện tích tam giác $\Large {A}'BC$ bằng $\Large 2a^2$ . Tính góc giữa hai mặt phẳng $\Large ({A}'BC)$ và $\Large (ABC)$ .

A. $\Large 45^{\circ}$ .
B. $\Large 120^{\circ}$ .
C. $\Large 30^{\circ}$ .
D. $\Large 60^{\circ}$ .

Đáp án án đúng là: C

Lời giải chi tiết:

Chọn C

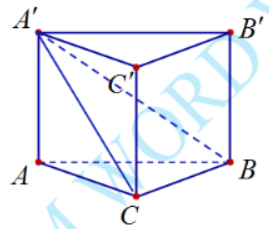
$Hình đáp án 1. Cho lăng trụ tam giác đều $\Large ABC.{A}'{B}'{C}'$ có diện tích đáy b$

Tam giác $\Large ABC$ là hình chiếu vuông góc của tam giác $\Large {A}'BC$ .

Gọi $\Large \alpha$ là góc giữa hai mặt phẳng $\Large ({A}'BC)$ và $\Large (ABC)$ thì $\Large \cos\alpha=\dfrac{S_{ABC}}{S_{{A}'BC}}=\dfrac{\sqrt{3}a^2}{2a^2}=\dfrac{\sqrt{3}}{2}\Rightarrow \alpha=30^{\circ}$ .

Bài sau

Xem thêm các bài tiếp theo bên dưới

Cho lăng trụ tam giác đều ABC.A′B′C′\Large ABC.{A}'{B}'{C}' có diện tích đáy b

Câu hỏi:

Cho lăng trụ tam giác đều ABC.A′B′C′\Large ABC.{A}'{B}'{C}' có diện tích đáy bằng √3a2\Large \sqrt{3}a^2, diện tích tam giác A′BC\Large {A}'BC bằng 2a2\Large 2a^2. Tính góc giữa hai mặt phẳng (A′BC)\Large ({A}'BC) và (ABC)\Large (ABC).

Đáp án án đúng là: C

Cho lăng trụ tam giác đều $\Large ABC.{A}'{B}'{C}'$ có diện tích đáy b

Cho lăng trụ tam giác đều $\Large ABC.{A}'{B}'{C}'$ có diện tích đáy bằng $\Large \sqrt{3}a^2$ , diện tích tam giác $\Large {A}'BC$ bằng $\Large 2a^2$ . Tính góc giữa hai mặt phẳng $\Large ({A}'BC)$ và $\Large (ABC)$ .