Cho hàm số y=√x có đồ thị (C) và điểm $\Large
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hàm số y=√x có đồ thị (C) và điểm M thuộc (C) có hoành độ dương. Gọi S1 là diện tích hình phẳng giới hạn bởi (C), trục hoành và đường thẳng đi qua M vuông góc với trục hoành; S2 là diện tích hình phẳng giới hạn bởi (C) và đường thẳng OM. Biết S2S1=ab (với a,b∈N∗ và ab là phân số tối giản), giá trị của a+b bằng
Đáp án án đúng là: C
Lời giải chi tiết:
Chọn C
Gọi M(m;√m)∈(C), (m>0).
Phương trình đường thẳng OM:y=1√mx.
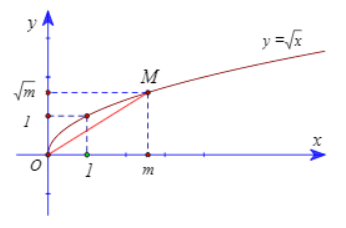
Ta có S1=m∫0|√x|dx=23√m3
S2=m∫0|√x−1√mx|dx=16√m3
⇒S2S1=14
Vậy a+b=5.
Xem thêm các bài tiếp theo bên dưới