Cho hình chóp $\Large S.ABC$ có đáy là tam giác vuông tại $\Large A$,

Cho hình chóp $\Large S.ABC$ có đáy là tam giác vuông tại $\Large A$, $\Large AB = a$, $\Large AC = 2a$, $\Large SA$ vuông góc với mặt phẳng đáy và $\Large SA = 2a$. Gọi $\Large G$ là trọng tâm của $\Large \Delta ABC$. Khoảng cách giữa hai đường thẳng $\Large SG$ và $\Large BC$ bằng

• A.

  A. $\Large \dfrac{2a}{7}$

• B.

  B. $\Large \dfrac{a\sqrt{6}}{3}$

• C.

  C. $\Large \dfrac{2a\sqrt{6}}{9}$

• D.

  D. $\Large \dfrac{4a}{7}$

Chọn A

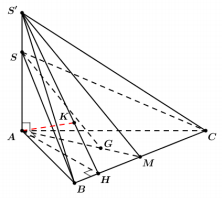
Gọi $\Large M$ là trung điểm của $\Large BC$. Trong mặt phẳng $\Large (SAM)$ dựng $\Large S{}'M // SG$. Suy ra: $\Large S{}'A = \dfrac{3}{2}SA = 3a$.

Do đó:

$\Large d(SG, BC) = d(SG, (S{}'BC)) = d(G,(S{}'BC)).$

Vì $\Large AM = 3GM$ nên $\Large d(G,(S{}'BC)) = \dfrac{1}{3}d(A,(S{}'BC))$.

Kẻ $\Large AH \bot BC$ ta có $\Large BC \bot (S{}'AH)$.

Kẻ $\Large AK \bot S{}'H$ $\Large \Rightarrow AK = d\left ( A,(S{}'BC) \right )$.

Ta có:

$\Large \dfrac{1}{AH^{2}} = \dfrac{1}{AB^{2}} + \dfrac{1}{AC^{2}} \Rightarrow AH = \dfrac{2a}{\sqrt{5}}$

Suy ra:

$\Large \dfrac{1}{AK^{2}} = \dfrac{1}{S{}'A^{2}} + \dfrac{1}{AH^{2}}$ 

$\Large \Rightarrow AK = \dfrac{6a}{7}$.

Do đó:

$\Large d\left ( S,(S{}'BC) \right ) = \dfrac{1}{3}AK = \dfrac{2a}{7}$.