Cho hình nón có chiều cao $\Large 6a$. Một mặt phẳng $\Large (P)$ đi q

Cho hình nón có chiều cao $\Large 6a$. Một mặt phẳng $\Large (P)$ đi qua đỉnh của hình nón và có khoảng cách đến tâm là $\Large 3a$, thiết diện thu được là một tam giác vuông cân. Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng

• A.

  A. $\Large 150 \pi a^{3}$

• B.

  B. $\Large 96 \pi a^{3}$

• C.

  C. $\Large 108 \pi a^{3}$

• D.

  D. $\Large 120 \pi a^{3}$

Chọn D

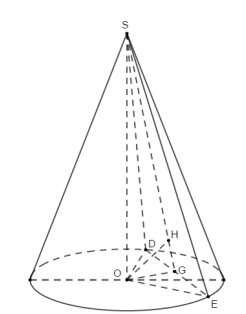
Mặt phẳng $\Large (P)$ cắt hình nón theo thiết diện là tam giác $\Large SDE$. Theo giả thiết, tam giác $\Large SDE$ vuông cân tại đỉnh $\Large S$. Gọi $\Large G$ là trung điểm $\Large DE$, kẻ $\Large OH \bot SG  OH = 3a$.

Ta có:

$\Large \dfrac{1}{OH^{2}} = \dfrac{1}{SO^{2}}+ \dfrac{1}{OG^{2}}$

$\Large \Rightarrow \dfrac{1}{OG^{2}} = \dfrac{1}{OH^{2}}- \dfrac{1}{SO^{2}}$

$\Large \Rightarrow OG = 2a\sqrt{3}$.

Do $\Large SO. OG = OH. SG$

$\Large  \Rightarrow SG = \dfrac{SO.OG}{SG} = \dfrac{6a.2a\sqrt{3}}{3a} = 4a\sqrt{3}$

$\Large  \Rightarrow DE = 8a\sqrt{3}$

$\Large OD = \sqrt{OG^{2} + DG^{2}} = \sqrt{12a^{2} + 48a^{2}} = 2\sqrt{15}a$

Vậy $\Large V = \dfrac{1}{3} . \pi . (2\sqrt{15}a)^{2} . 6a = 120 \pi a^{3}$.