Cho hàm số $\Large y = \dfrac{ax + b}{cx + 1}$ $\Large (a, b, c \in \m

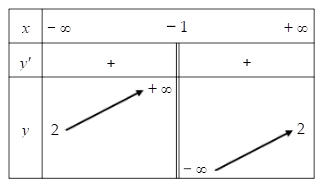
Cho hàm số $\Large y = \dfrac{ax + b}{cx + 1}$ $\Large (a, b, c \in \mathbb{R})$ có bảng biến thiên như sau:

Tập các giá trị $\Large b$ là tập nghiệm của bất phương trình nào dưới đây?

• A.

  A. $\Large b^{3} - 8 \leq 0$

• B.

  B. $\Large -b^{2} + 4 > 0$

• C.

  C. $\Large b^{2} - 3b + 2 < 0$

• D.

  D. $\Large b^{3} - 8 < 0$

Chọn D

Đồ thị hàm số $\Large y = \dfrac{ax + b}{cx + 1}$ có đường tiệm cận đứng là đường $\Large x = -\dfrac{1}{c}$ và đường tiệm cận ngang là đường thẳng $\Large y = \dfrac{a}{c}$.

Nhìn vào bảng biến thiên, ta thấy $\Large -\dfrac{1}{c} = -1 \Rightarrow c = 1$ và $\Large \dfrac{a}{c} = 2 \Rightarrow a = 2$ (vì $\Large c = 1$).

Ta có:

$\Large y{}' = \dfrac{a - bc}{(cx + 1)^{2}}$.

Vì hàm số đồng biến trên các khoảng $\Large (-\infty ; -1)$ và $\Large (-1; +\infty)$ nên 

$\Large y{}' = \dfrac{a - bc}{(bx + c)^{2}} > 0$ 

$\Large \Leftrightarrow a - bc > 0$ 

$\Large \Leftrightarrow 2 - b > 0$ 

$\Large \Leftrightarrow b < 2$ 

$\Large \Leftrightarrow b^{3} < 8$ 

$\Large \Leftrightarrow b^{3} - 8 < 0$.

Vậy tập các giá trị $\Large b$ là tập nghiệm của bất phương trình $\Large b^{3} - 8 < 0$.