Cho hàm số $\Large f(x) = \left | x^{4} - 2x^{3} + x^{2} + m \right |$

Cho hàm số $\Large f(x) = \left | x^{4} - 2x^{3} + x^{2} + m \right |$ ($\Large m$ là tham số thực). Gọi $\Large S$ là tập hợp tất cả các giá trị của $\Large m$ sao cho $\Large \min_{\left [ -1; 2 \right ]}f(x) + \max_{\left [ -1; 2 \right ]}f(x) = 10$. Số phần tử của $\Large S$ là?

• A.

  A. 2

• B.

  B. 3

• C.

  C. 5

• D.

  D. 1

Chọn A

Đặt $\Large g(x) = x^{4} - 2x^{3} + x^{2} + m$

$\Large \Rightarrow g{}'(x) = 4x^{3} - 6x^{2} + 2x = 0$ 

$\Large \Leftrightarrow \left[\begin{array}{l}x=0 \\x=\dfrac{1}{2} \\x=1\end{array}\right.$

Bảng biến thiên của hàm số $\Large g(x)$:

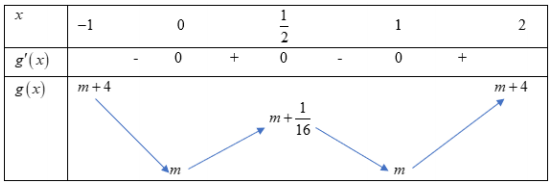
Dựa vào bảng biến thiên của $\Large g(x)$ ta suy ra bảng biến thiên của $\Large f(x) = \left | g(x) \right | = \left | x^{4} - 2x^{3} + x^{2} + m \right |$. Ta có các trường hợp sau:

Trường hợp 1: $\Large m \geq 0$. Bảng biến thiên của $\Large f(x) = \left | g(x) \right | = \left | x^{4} - 2x^{3} + x^{2} + m \right |$

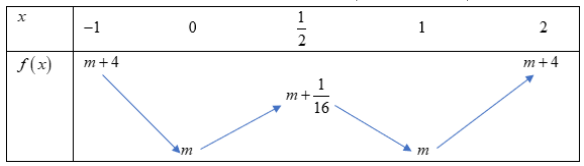
Dựa vào bảng biến thiên ta có:

$\Large \min_{\left [ -1; 2 \right ]}f(x) + \max_{\left [ -1; 2 \right ]}f(x) = 10$

$\Large \Leftrightarrow m + m + 4 = 10$

$\Large \Leftrightarrow m = 3$ (TM).

Trường hợp 2: $\Large m < 0 < m + \dfrac{1}{16}$

$\Large \Leftrightarrow -\dfrac{1}{16} < m < 0$

Bảng biến thiên:

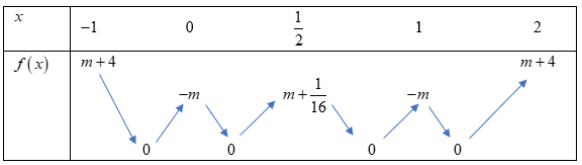
Dựa vào bảng biến thiên ta có:

$\Large \min_{\left [ -1; 2 \right ]}f(x) + \max_{\left [ -1; 2 \right ]}f(x) = 10$

$\Large \Leftrightarrow 0 + m + 4 = 10$

$\Large \Leftrightarrow m = 6$ (Loại).

Trường hợp 3: $\Large m + \dfrac{1}{16} = 0$ 

$\Large \Leftrightarrow m = -\dfrac{1}{16}$

Tương tự ta có:

$\Large \min_{\left [ -1; 2 \right ]}f(x) + \max_{\left [ -1; 2 \right ]}f(x) = 10$

$\Large \Leftrightarrow 0 + m + 4 = 10$

$\Large \Leftrightarrow m = 6$ (Loại).

Trường hợp 4: $\Large m + \dfrac{1}{16} < 0 < m + 4$ 

$\Large \Leftrightarrow -4 < m < -\dfrac{1}{16}$

Bảng biến thiên:

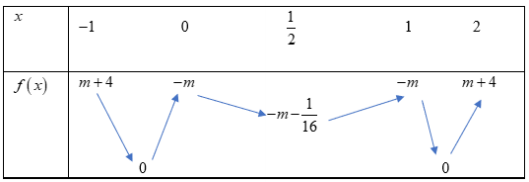
Dựa vào bảng biến thiên ta có:

$\Large \left[\begin{array}{l}\min_{\left [ -1; 2 \right ]}f(x) + \max_{\left [ -1; 2 \right ]}f(x) = 10 \\\min_{\left [ -1; 2 \right ]}f(x) + \max_{\left [ -1; 2 \right ]}f(x) = 10 \\\end{array}\right.$

$\Large \Leftrightarrow \left[\begin{array}{l}0 + m + 4 = 10 \\ 0 + (-m) = 10 \\\end{array}\right.$

$\Large \Leftrightarrow \left[\begin{array}{l} m = 6 \\ m = -10 \\\end{array}\right.$ (Loại)

Trường hợp 5: $\Large m + 4 = 0  \Leftrightarrow m = -4$. Ta có:

$\Large \min_{\left [ -1; 2 \right ]}f(x) + \max_{\left [ -1; 2 \right ]}f(x) = 10$

$\Large \Leftrightarrow 0 -m = 10$

$\Large \Leftrightarrow m = -10$ (Loại).

Trường hợp 6: $\Large m + 4 < 0  \Leftrightarrow m < -4$. Ta có:

$\Large \min_{\left [ -1; 2 \right ]}f(x) + \max_{\left [ -1; 2 \right ]}f(x) = 10$

$\Large \Leftrightarrow -m -m - 4 = 10$

$\Large \Leftrightarrow m = -7$ (Thỏa mãn).

Vậy $\Large m \in$ {-7; 3}.