Cho hình chóp tứ giác đều $\Large S.ABCD$ có cạnh đáy bằng $\Large a$,

Cho hình chóp tứ giác đều $\Large S.ABCD$ có cạnh đáy bằng $\Large a$, góc $\Large \widehat{SAB} = 60^{\circ}.$ Thể tích của hình nón đỉnh $\Large S$ đáy là đường tròn ngoại tiếp $\Large ABCD$ là:

• A.

  A. $\Large \dfrac{\pi a^{3} \sqrt{2}}{12}.$

• B.

  B. $\Large \dfrac{\pi a^{3} \sqrt{3}}{6}.$

• C.

  C. $\Large \dfrac{\pi a^{3} \sqrt{3}}{12}.$

• D.

  D. $\Large \dfrac{\pi a^{3} \sqrt{2}}{6}.$

Chọn A

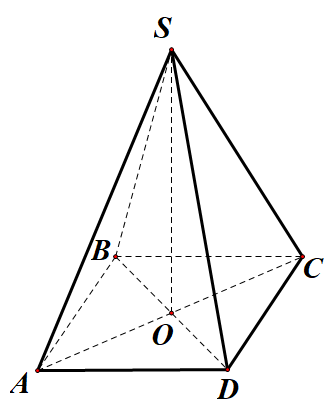
$\Large S.ABCD$ là hình chóp đều nên các mặt bên là tam giác cân, kết hợp giả thiết $\Large \widehat{SAB} = 60^{o}$ suy ra tam giác $\Large SAB$ là tam giác đều. Tính được độ dài đường cao của $\Large S.ABCD$ là

$\Large SO = \sqrt{SA^2-AO^2}$ $\Large =\sqrt{a^2-\left(\dfrac{a\sqrt{2}}{2}\right)^2}$ $\Large =\dfrac{a \sqrt{2}}{2}.$

Hình nón đỉnh $\Large S$ đáy là đường tròn ngoại tiếp $\Large ABCD$ có đường cao bằng  $\Large SO = \dfrac{a \sqrt{2}}{2}$ và bán kính đáy bằng  $\Large r = \dfrac{a \sqrt{2}}{2}.$

Vậy thể tích của khối nón giới hạn bởi hình chóp đó là

$\Large \dfrac{1}{3}\pi r^2h$ $\Large =\dfrac{1}{3}\pi \left(\dfrac{a\sqrt{2}}{2}\right)^2.\dfrac{a\sqrt{2}}{2}$ $\Large =\dfrac{\pi a^{3} \sqrt{2}}{12}.$