Cho hình hộp $\Large ABCD.A{}'B{}'C{}'D{}'$ có chiều cao 8 và diện tíc

Cho hình hộp $\Large ABCD.A{}'B{}'C{}'D{}'$ có chiều cao 8 và diện tích đáy bằng 11. Gọi $\Large M$ là trung điểm của $\Large AA{}'$, $\Large N$ là điểm trên cạnh $\Large BB{}'$ sao cho $\Large BN = 3.B{}'N$ và $\Large P$ là điểm trên cạnh $\Large CC{}'$ sao cho $\Large 6CP = 5.C{}'P$. Mặt phẳng $\Large(MNP)$ cắt cạnh $\Large DD{}'$ tại $\Large Q$. Thể tích của khối đa diện lồi có các đỉnh là các điểm $\Large A, B, C, D, M, N, P$ và $\Large Q$ bằng

• A.

  A. $\Large \dfrac{88}{3}$

• B.

  B. $\Large 42$

• C.

  C. $\Large 44$

• D.

  D. $\Large \dfrac{220}{3}$

Chọn B

Trước tiên ta chứng minh bổ đề sau:

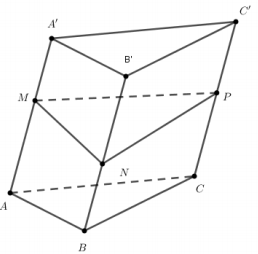
Cho lăng trụ như hình vẽ, $\Large V_{ABC.MNP} = \dfrac{1}{3}\left ( \dfrac{AM}{AA{}'}+\dfrac{BN}{BB{}'} + \dfrac{CP}{CC{}'}\right ). V_{ABC.A{}'B{}'C{}'}$.

Chứng minh:

$\Large V_{ABC.MNP} = V_{N.ABC} + V_{N.ACPM}$

$\Large V_{N.ABC} = \dfrac{BN}{BB{}'}.V_{B{}'.ACB} = \dfrac{BN}{BB{}'}. \dfrac{1}{3}. V_{ABC.A{}'B{}'C{}'}$

$\Large \dfrac{V_{N.ACPM}}{V_{B{}'}.ACC{}'A{}'} = \dfrac{S_{ACPM}}{S_{ACC{}'A{}'}}$ 

$\Large = \dfrac{\dfrac{1}{2}.(CP+AM)}{AA{}'} = \dfrac{1}{2}.\left ( \dfrac{CP}{CC{}'}+\dfrac{AM}{AA{}'} \right )$.

$\Large \Rightarrow V_{N.ACPM} = \dfrac{1}{2}.\left ( \dfrac{CP}{CC{}'}+\dfrac{AM}{AA{}'} \right ).\dfrac{2}{3}.V_{ABC.A{}'B{}'C{}'}$.

Từ đó suy ra điều phải chứng minh.

Bây giờ ta áp dụng vào bài toán.

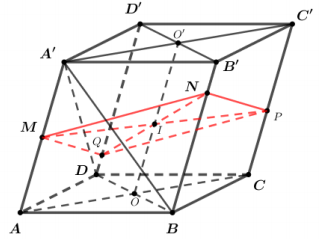
Ta có:

$\Large \left\{\begin{matrix} (ADD{}'A{}'') // (BCC{}'B{}')\\ MQ \subset (MNP) \cap (ADD{}'A{}')\Rightarrow NP // MQ \\ NP\subset (MNP) \cap (BCC{}'B{}')\end{matrix}\right.$

Do đó $\Large MNPQ$ là hình bình hành.

Ta có $\Large OI$ là đường trung bình của hai hình thang $\Large AMPC$ và $\Large BNQD$ suy ra:

$\Large 2OI = MA + PC = DQ + NB$

$\Large \Rightarrow \dfrac{MA}{AA{}'} + \dfrac{PC}{CC{}'} = \dfrac{BN}{BB{}'} + \dfrac{DQ}{DD{}'}$

Dựa vào hình vẽ ta chia khối lăng trụ làm hai phần khi cắt  bởi mặt phẳng $\Large (BDD{}'B{}')$. Do đó:

$\Large V_{A{}'D{}'B{}'.ADB} = V_{BD{}'C{}'.BDC} = 44$

$\Large V_{ABCD.MNPQ} = V_{ABD.MNQ} + V_{BCD.NPQ}$.

$\Large = \dfrac{1}{3} \left ( \dfrac{MA}{AA{}'} + \dfrac{BN}{BB{}'} + \dfrac{DQ}{DD{}'} \right ).V_{ABD.A{}'B{}'D{}'} + \dfrac{1}{3}\left ( \dfrac{CP}{CC{}'} + \dfrac{BN}{BB{}'} + \dfrac{DQ}{DD{}'}\right ).V_{BCD.B{}'C{}'D{}'}$

$\Large = \dfrac{1}{3} \left ( \dfrac{MA}{AA{}'} + \dfrac{BN}{BB{}'} + \dfrac{DQ}{DD{}'} + \dfrac{CP}{CC{}'} + \dfrac{BN}{BB{}'} + \dfrac{DQ}{DD{}'}\right ).\dfrac{1}{2}.V_{ABC.A{}'B{}'C{}'} $

$\Large = \dfrac{1}{3.2}.\left [ 3.\left ( \dfrac{MA}{AA{}'} + \dfrac{CP}{CC{}'} \right ) \right ].V_{ABC.A{}'B{}'C{}'}$

$\Large = \dfrac{1}{2}.\left ( \dfrac{1}{2}+\dfrac{5}{11} \right ).88$

$\Large =42$.