Cho hình chóp có đáy là tam giác vuông tại $\large A, A
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp có đáy là tam giác vuông tại . Cạnh bên vuông góc với mặt phẳng đáy. Gọi là trung điểm của tạo với mặt phẳng đáy góc . Thể tích của khối chóp đã cho bằng
Đáp án án đúng là: D
Lời giải chi tiết:
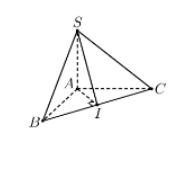
Xác định:
Ta có: và
Diện tích tam giác:
Vậy thể tích khối chóp: .
Chọn D