Cho hình chóp $\Large S.ABC$ có đáy là tam giác đều, $\Large AB=2a$, $

Cho hình chóp $\Large S.ABC$ có đáy là tam giác đều, $\Large AB=2a$, $\Large SA$ vuông góc với mặt phẳng đáy, $\Large SA=a\sqrt{3}$. Góc giữa hai mặt phẳng $\Large (SBC)$ và $\Large (ABC)$ là

• A.

  $\Large 60^{\circ}$.

• B.

  $\Large 30^{\circ}$.

• C.

  $\Large 120^{\circ}$.

• D.

  $\Large 45^{\circ}$.

Chọn D

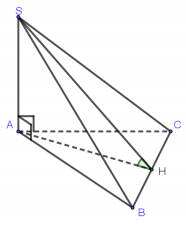
Gọi $\Large H$ là trung điểm cạnh $\Large BC$, khi đó $\Large \left\{\begin{align} & BC\perp AH \\ & BC\perp SA \end{align}\right.$ $\Large \Rightarrow BC\perp (SAH)\Rightarrow BC\perp SH$.

Vậy $\Large \left\{\begin{align} & (SBC)\cap (ABC)=BC \\ & BC\perp SH \\ & BC\perp AH \end{align}\right.$ nên góc giữa hai mặt phẳng $\Large (SBC)$ và $\Large (ABC)$ là $\Large \widehat{SHA}$.

Trong tam giác vuông $\Large SAH$ có $\Large tan\widehat{SAH}=\dfrac{SA}{AH}=\dfrac{a\sqrt{3}}{a\sqrt{3}}=1\Rightarrow \widehat{SHA}=45^{\circ}$. Vậy $\Large \widehat{\big((SBC), (ABC)\big)}=45^{\circ}$.