Cho hình chóp đều S.ABCD, $\Large SA=AB=2a$ (minh họa như hình bên dướ

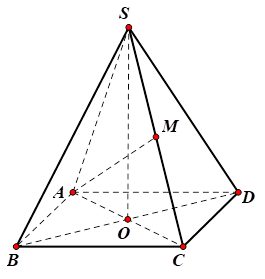
Cho hình chóp đều S.ABCD, $\Large SA=AB=2a$ (minh họa như hình bên dưới). Gọi M là trung điểm của SC. Khoảng cách giữa hai đường thẳng AM và CD bằng

• A.

  $\Large \dfrac{2\sqrt{2}a}{3}.$

• B.

  $\Large \dfrac{2\sqrt{10}a}{9}.$

• C.

  $\Large \dfrac{2\sqrt{22}a}{11}.$

• D.

  $\Large a.$

Chọn C

ABCD là hình vuông $\Large \Rightarrow AO=\dfrac{AC}{2}=\dfrac{2a\sqrt{2}}{2}=a\sqrt{2}.$

$\Large SO=\sqrt{SA^2-AO^2}=\sqrt{(2a)^2-(a\sqrt{2})^2}=a\sqrt{2}.$

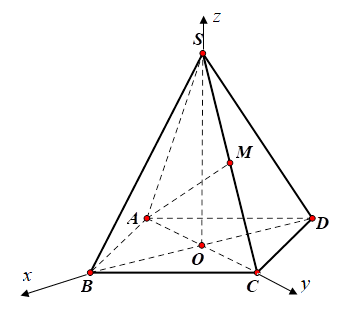
Gắn hệ trục tọa độ với O là gốc tọa độ, OB nằm trên trục Ox, OC nằm trên trục Oy, SO nằm trên trục Oz.

Ta có $\Large A (0; -\sqrt{2}a; 0), C (0; \sqrt{2}a; 0), D (-\sqrt{2}a; 0; 0), S (0; 0; \sqrt{2}a).$

Vì M là trung điểm SC $\Large \Rightarrow M \left(0; \dfrac{\sqrt{2}a}{2}; \dfrac{\sqrt{2}a}{2}\right).$

$\Large \overrightarrow{AM}=\left(0; \dfrac{3\sqrt{2}a}{2}; \dfrac{\sqrt{2}a}{2}\right), \overrightarrow{CD}=\left(-\sqrt{2}a; -\sqrt{2}a; 0\right), \overrightarrow{AC}=\left(0; 2\sqrt{2}a; 0\right).$

$\Large \left[\overrightarrow{AM}, \overrightarrow{CD}\right]=(a^2; -a^2; 3a^2) \Rightarrow |\left[\overrightarrow{AM}, \overrightarrow{CD}\right]|=\sqrt{11}a^2.$

$\Large \left[\overrightarrow{AM}, \overrightarrow{CD}\right].\overrightarrow{AC}=a^2.0+(-a^2).2\sqrt{2}a+3a^2.0=-2\sqrt{2}a^3.$

$\Large d(AM, CD)=\dfrac{|\left[\overrightarrow{AM}, \overrightarrow{CD}\right].\overrightarrow{AC}|}{|\left[\overrightarrow{AM}, \overrightarrow{CD}\right]|}=\dfrac{|-2\sqrt{2}a^3|}{\sqrt{11}a^2}=\dfrac{2\sqrt{22}}{11}a.$