Cho hàm số $\Large y=f(x)$ có đạo hàm liên tục trên $\Large \mathbb{R}

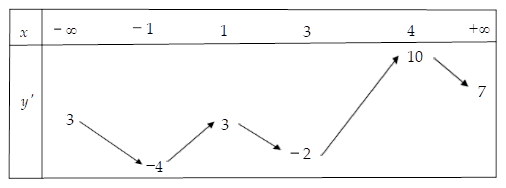
Cho hàm số $\Large y=f(x)$ có đạo hàm liên tục trên $\Large \mathbb{R}$ và có bảng biến thiên của $\Large {f}'(x)$ như sau:

Có bao nhiêu số nguyên của m để hàm số $\Large g(x)=f(x)-mx$ nghịch biến trên khoảng $\Large (-\infty; 3),$ đồng thời đồng biến trên khoảng $\Large (4; +\infty)?$

• A. 4.
• B. 3.
• C. 5.
• D. 6.

Chọn A

Ta có $\Large {g}'(x)={f}'(x)-m$

Để hàm số nghịch biến trên khoảng $\Large (-\infty; 3)$ thì

$\Large {g}'(x) \leq 0, \forall x \in (-\infty; 3) \Leftrightarrow {f}'(x) \leq m, \forall x \in (-\infty; 3) \Rightarrow m \geq 3$

Để hàm số đồng biến trên khoảng $\Large (4; +\infty)$ thì 

$\Large {g}'(x) \geq 0, \forall x \in (4; +\infty) \Leftrightarrow {f}'(x) \geq m, \forall x \in (4; +\infty) \Rightarrow m \leq 7.$

$\Large \Rightarrow m \in [3; 7] \Rightarrow m \in \begin{Bmatrix} 
3; 4; 5; 6; 7
\end{Bmatrix}.$ Vậy có 5 giá trị nguyên của m.